Question

$ \Delta AMT\sim \Delta AHE $ . In $ \Delta AMT $ , AM = 6.3cm, $ \angle MAT={{120}^{\circ }} $ , AT = 4.9cm and $ \dfrac{MA}{HA}=\dfrac{7}{5} $ . Construct both the triangles.

Answer 1

Hint: In this question, we are given an angle, two sides of a triangle $ \Delta AMT $ and $ \Delta AMT $ is similar to $ \Delta AHE $ such that $ \dfrac{MA}{HA}=\dfrac{7}{5} $ . For construction, we will first draw $ \Delta AMT $ using given measurements and then we will construct $ \Delta AHE $ whose sides will be $ \dfrac{7}{5} $ of corresponding sides of $ \Delta AMT $ . We will write the steps of construction to understand better.

Complete step by step answer:
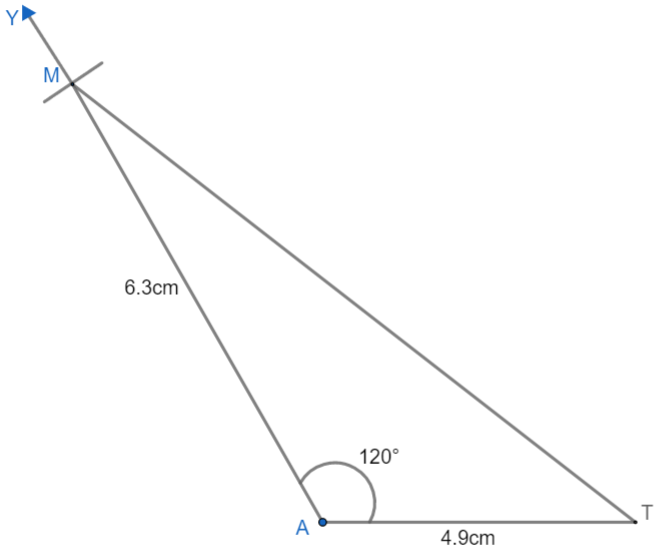
Let us first draw $ \Delta AMT $ having sides AM = 6.3cm, $ \angle MAT={{120}^{\circ }} $ , AT = 4.9cm.
Steps of construction for drawing $ \Delta AMT $.
(i) Firstly, let us draw a line segment AT = 4.9cm using a ruler.
(ii) Now with A as the center, let us draw an angle of $ {{120}^{\circ }} $ such that $ \angle YAT={{90}^{\circ }} $ .
(iii) Now with A as center and compass opened with 6.3cm radius, let’s draw an arc on the ray AY which cuts the ray AY at some point M.

(iv) Join M to T. We get our required triangle $ \Delta AMT $ which looks like this,

Now we need to draw a $ \Delta AHE $ which is similar to $ \Delta AMT $ . We are given that, $ \dfrac{MA}{HA}=\dfrac{7}{5} $ . We know from the similarity of triangles, that all corresponding sides are proportional. So for $ \Delta AMT\text{ and }\Delta AHE $ we can say that $ \dfrac{MA}{HA}=\dfrac{MT}{HE}=\dfrac{AT}{AE}=\dfrac{7}{5} $ or we can write it as $ \dfrac{HA}{MA}=\dfrac{HE}{MT}=\dfrac{AE}{AT}=\dfrac{5}{7} $ .
Hence all the sides are proportional. So $ \Delta AHT $ is $ {{\dfrac{5}{7}}^{th}} $ of the triangle $ \Delta AMT $ . Let us draw $ \Delta AHT $ such that $ \Delta AHT $ is $ {{\dfrac{5}{7}}^{th}} $ of $ \Delta AHT $ following are the steps of construction.
(i) From A, let us draw any ray AX which makes some acute angle with side AT on the opposite to vertex M.
(ii) Then let us mark 7 points $ {{B}_{1}},{{B}_{2}},{{B}_{3}},{{B}_{4}},{{B}_{5}},{{B}_{6}},{{B}_{7}} $ on AX such that $ A{{B}_{1}}={{B}_{1}}{{B}_{2}}={{B}_{2}}{{B}_{3}}={{B}_{3}}{{B}_{4}}={{B}_{4}}{{B}_{5}}={{B}_{5}}{{B}_{6}}={{B}_{6}}{{B}_{7}} $ .
For this, we shall keep the radius of the compass equal and draw the arc.
(iii) Now let us join $ {{B}_{7}} $ with T. Now from $ {{B}_{5}} $ draw a line to cut the side AT at point E such that $ {{B}_{5}}E $ is parallel to $ {{B}_{7}}T $ .
(iv) Now from E point, draw a line to cut the side AM at H such that EH is parallel to MT.
Triangle $ \Delta AEH $ is our required triangle which looks like this,

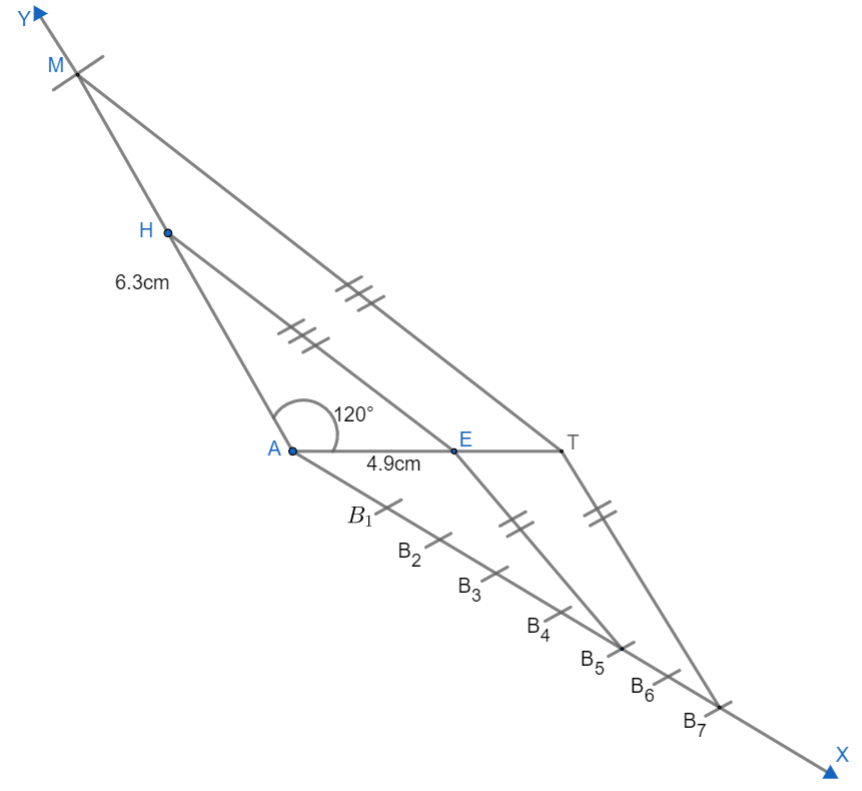
These are our required triangles.
Note:
Students often make the mistake of assuming $ \Delta AHE $ as $ {{\dfrac{7}{5}}^{th}} $ of $ \Delta AMT $ but it is the opposite. Students should note that in a similar triangle all corresponding angles are equal. So they can check their drawn triangles. Make sure pencils are sharped and the compass is tight. Students should know how to draw angles (like $ {{60}^{\circ }},{{120}^{\circ }} $ ) and parallel lines.