Question

How many degrees are in the sum of measures of complementary angles?

Answer 1

Hint: As we know that the complementary angles are the two angles that are complement to one another means the sum of those angles are \[90{}^\circ \]. When a line divides a right angle then these two angles will be termed as the complementary angles. Let suppose the angle bisector of a right angle then the bisected angles will be of \[45{}^\circ \] each, then these two angles are complementary to another.

Complete step by step solution:
Since there are many special relations that can be formed using angles.
And one of the relation is complementary angles

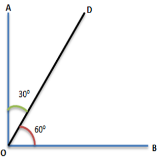
Given that, \[OA\bot OB\]
\[\Rightarrow \angle AOB=90{}^\circ \]
Also,
 \[\begin{align}
  & \angle AOD=30{}^\circ \\
 & \angle DOB=60{}^\circ \\
\end{align}\]

Here, \[\angle AOD\] and \[\angle DOB\] are the complementary angles as the sum of these angles are \[90{}^\circ \].

Note:
The complementary angles are the angles which are complement to one another and the sum of these angles are \[90{}^\circ \]. Means when we say these two angles are complementary then their sum must be of \[90{}^\circ \]. In case of angle bisectors these two angles are equal and will be equal to \[45{}^\circ \] each as the angle bisector bisects the angle means divide the angle in two equal measures.