Question

What is the definition of a coordinate proof? And what is an example?

Answer 1

Hint: We know that the proof of a geometric theorem that uses generalized points on the Cartesian plane to make an argument.

Complete step-by-step solution:
We know that there are situations when we use numbers, variables or algebraic equations instead of the geometric shapes including circles, lines, points, etcetera.
Let us suppose that we need to prove a geometric theorem and we are using the algebraic equations and variables to prove the theorem. Such a proof is called a coordinate proof.
We define the coordinate proof of a geometric theorem as a proof that uses algebraic expressions.
Let us give an example of the coordinate proof.
Let us recall the geometric theorem named as Midline Theorem which states that the midpoints of sides of any quadrilateral form a parallelogram.
Let us suppose that the four points $A\left( {{x}_{A}},{{y}_{A}} \right),B\left( {{x}_{B}},{{y}_{B}} \right),C\left( {{x}_{C}},{{y}_{C}} \right)$ and $D\left( {{x}_{D}},{{y}_{D}} \right)$ are the vertices of a quadrilateral.
Now, let us write the coordinates of the midpoints of the sides of the quadrilateral $ABCD.$
We will get the midpoint $P$ of the side $AB$ as $\left( {{x}_{P}}=\dfrac{{{x}_{A}}+{{x}_{B}}}{2},{{y}_{P}}=\dfrac{{{y}_{A}}+{{y}_{B}}}{2} \right).$
We will get the midpoint $Q$ of the side $BC$ as $\left( {{x}_{Q}}=\dfrac{{{x}_{B}}+{{x}_{C}}}{2},{{y}_{Q}}=\dfrac{{{y}_{B}}+{{y}_{C}}}{2} \right).$
We will get the midpoint $R$ of the side $CD$ as $\left( {{x}_{R}}=\dfrac{{{x}_{C}}+{{x}_{D}}}{2},{{y}_{R}}=\dfrac{{{y}_{C}}+{{y}_{D}}}{2} \right).$
We will get the midpoint $S$ of the side $DA$ as $\left( {{x}_{S}}=\dfrac{{{x}_{D}}+{{x}_{A}}}{2},{{y}_{S}}=\dfrac{{{y}_{D}}+{{y}_{A}}}{2} \right).$
We will show that opposite sides are parallel which is a sufficient condition for a parallelogram.
First, we will show the side $PQ$ is parallel to the side $RS$ by showing that their slopes are the same.
Now, we will get the slope of $PQ$ as $\dfrac{{{y}_{Q}}-{{y}_{P}}}{{{x}_{Q}}-{{x}_{P}}}=\dfrac{{{y}_{A}}+{{y}_{D}}-{{y}_{A}}-{{y}_{B}}}{{{x}_{A}}+{{x}_{D}}-{{x}_{A}}-{{x}_{B}}}=\dfrac{{{y}_{D}}-{{y}_{B}}}{{{x}_{D}}-{{x}_{B}}}$
We will get the slope of $RS$ as $\dfrac{{{y}_{S}}-{{y}_{R}}}{{{x}_{S}}-{{x}_{R}}}=\dfrac{{{y}_{C}}+{{y}_{D}}-{{y}_{C}}-{{y}_{B}}}{{{x}_{C}}+{{x}_{D}}-{{x}_{C}}-{{x}_{B}}}=\dfrac{{{y}_{D}}-{{y}_{B}}}{{{x}_{D}}-{{x}_{B}}}.$
Therefore, the slopes of the above sides are the same.
Similarly, we can show the side $PR$ is parallel to the side $QS$ by showing that their slopes are the same.

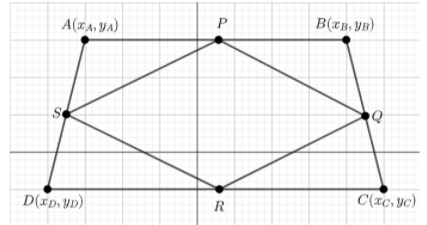
We know that this is the sufficient condition for a parallelogram
Hence we have proved the geometric theorem algebraically.

Note: We know that a parallelogram is also a quadrilateral where the opposite sides are parallel. As we know, the difference between the parallelograms and the rectangles is that all the angles of a rectangle are the same whereas the opposite angles of a parallelogram are the same but adjacent are not.