Question

Define the moment of force and state its SI unit.

Answer 1

Hint: The moment of a physical quantity is the rotational capability of that quantity. It is generally a cross product of the quantity with the distance from the axis at which it acts. Since the dimension of force and distance are known, we can easily find the unit of moment of force.

Complete step-by-step solution -
The term moment refers to the ability to create a rotation. The moment of force is the ability of a Force to create a rotation in a body. More precisely, we can say to increase or decrease the rotating speed.
We know that it is easier to close a door by pushing at the edge far away from the hinge than by pushing near the hinge. Here hinge is the axis of rotation of the body and we can see that the farther we are from the axis, the more the force we have to put in. That means that a high force alone is not enough to produce rotation. Where the force acts also determine the rotational effect. Similarly, it is also obvious that pushing perpendicular to the hinge produces maximum rotation, and if we push along the plane of the door and towards the hinge, no matter how high the force is, No rotations happen.

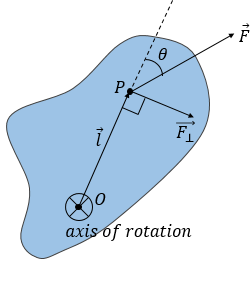
So we define the rotational effect of a force as the product of the perpendicular component force applied and the distance from the axis at which the force is applied.
This is the moment of force and it is also called torque. It is represented by the letter $\tau $.
$\tau = F \cdot {x_ \bot }$
We can see from the diagram that if $l$ is the distance from the axis where the force is applied, then ${x_ \bot } = lsin\theta $. This gives
$\tau = F \cdot l\sin \theta $
This is similar to a cross product and hence, we can also define the torque as :
$\vec \tau = \vec F \times \vec l$
Now since Force has a unit of Newton and SI unit of Length is meters, the moment of torque has the SI unit Newton-meter $Nm$.

Note: The SI unit of Torque is dimensionally the same as that of work. But we can neither use it as a unit for Torque nor equate them mathematically. These quantities have similar dimensions but represent different physical quantities.