Question

Define the circle segment and sector of a circle.

Answer 1

Hint: Make use of the standard definition of the segment of a circle which says the segment of a circle is the region bounded by a chord and the arc subtended by the chord.
Sector of the circle looks like a pizza slice.


Complete step by step solution: Segment is the region of a circle bounded by chord and an arc.

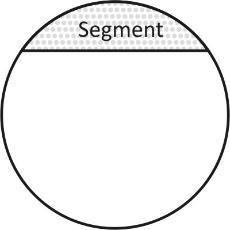
The segments are explained in two parts:
In the above diagram, a chord divided the circle in two parts in which the biggest part of the circle is known as the major segment and the smaller part is known as minor segment.
We also calculate the area of segment:

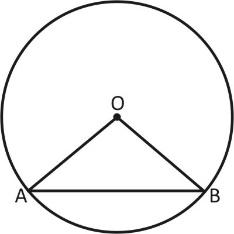
\[Area\,\,of\,\,segment = \dfrac{{\left( {\theta - \sin \theta } \right) \times {r^2}}}{2}\,\,\left[ {When\,\,\theta \,\,in\,\,radians} \right]\]
Area of segment$ = $Area of a sector $ - $Area of a triangle
\[Area\,\,of\,\,segment = \dfrac{{\theta \times \pi }}{{360}}{r^2} - \dfrac{{\sin \theta }}{2}{r^2}\] (When \[\theta \]is in degrees)
Sector of Circle:
The shaded region is the sector of the circle.

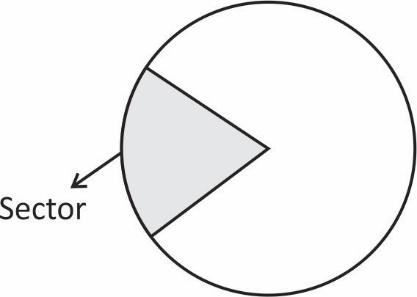
A sector is created by the central angle formed with two radii and it includes the area inside the circle from that center point to the circle itself. The portion of the circles circumference bounded by the radii, the arc, is part of the sector.
Common Sectors

The quadrant and semicircle are two special types of sector:

Area of sector\[ = \left( {\dfrac{{\theta ^\circ }}{{360^\circ }}} \right) \times \pi \times {r^2}\]
Where
\[\theta ^\circ \] = degree of the circle
\[{\text{r }} = {\text{ }}radius{\text{ }}of{\text{ }}the{\text{ }}circle\]

Note: A circle has an angle of\[2\pi \]and an area of${\text{\pi }}{{\text{r}}^{\text{2}}}$. A sector has an angle of\[\theta \]instead of \[2\pi \] so its area is:\[\dfrac{\theta }{{2\pi }} \times \pi {r^2}\]
Which can be simplified to:\[\dfrac{\theta }{2} \times {r^2}\].