Question

Define Raoult’s Law for the elevation of boiling point of a solution.

Answer 1

Hint:According to Raoult's law, elevation of boiling point of a solution is directly proportional to the lowering in vapour pressure caused by the number of particles of solute present in the solution.

\[\Delta {T_b} = \dfrac{{{K_b} \times {w_B} \times 1000}}{{{M_B} \times {w_A}}}\]
$\Delta {T_b} = {K_b} \times m$
Where,
$\Delta {T_b}$= Boiling point elevation
${K_b}$= Molal boiling point elevation constant ( also called ebullioscopic constant )
${w_b}$= given weight of solute
${M_b}$= Molecular mass of solute
${w_A}$= Given weight of solvent
$m$= molarity of solution

Complete step by step answer:
Elevation in boiling point:
The boiling point of a liquid is the temperature at which the vapour pressure of the liquid becomes equal to the atmospheric pressure.
For Example, vapour pressure of water is $1atm$ at $373K$. Therefore, water boils at $373K$ because its vapour pressure at this temperature becomes equal to one atmospheric pressure which is $1.013bar$. The vapour pressure of an aqueous solution of sucrose is less than $1.013bar$ at $373K$ and therefore the solution will not boil at $373K$.
In order to make the solution boil, its temperature must be increased so that its vapour pressure becomes equal to $1atm$. Thus, boiling point of a solution is always higher than the boiling point of the pure solvent in which the solvent is prepared.

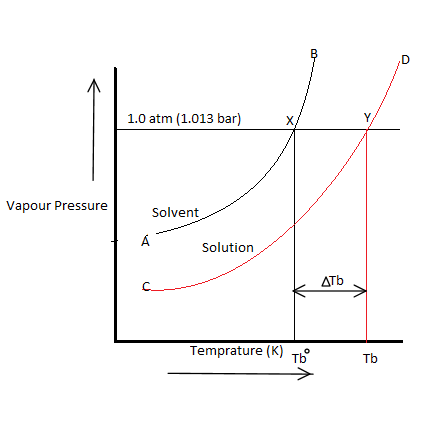
The elevation in boiling point on the addition of a non-volatile solute to a solvent can be easily illustrated graphically as shown above.
It is clear from the figure that the vapour pressure of the pure solvent becomes equal to atmospheric pressure at $X$ ( corresponding to temperature ${T_b}^0$) while the vapour pressure of the solution becomes equal to atmospheric pressure at $Y$( corresponding to the temperature ${T_b}$).
$\Delta {T_b} = {T_b} - {T_b}^0$

Note:
For a solution of two liquids A and B, Raoult's law predicts that if no other gases are present, then the total vapor pressure $p$ above the solution is equal to the weighted sum of the "pure" vapor pressures ${p_A}$ and ${p_B}$ of the two components. Hence, the total pressure above the solution of A and B would be:
$p = {p_A}{\chi _A} + {p_B}{\chi _B}$