Question

Define greatest integer function. Also write its graph. Domain and Range of the function.

Answer 1

Hint: Here we will proceed by using the approach of greatest integer function that is when the intervals are in the form of $\left( {n,n + 1} \right)$, the value of greatest integer function is $n$, where $n$ is an integer.

Complete Step-by-step answer:
The greatest integer function is represented or denoted by $\left[ x \right]$, for any real function. The function rounds-off the real number down to the integer less than the number. This function is also known as the Floor function.
For example,
$
  \left[ {1.15} \right] = 1 \\
  \left[ {4.56567} \right] = 4 \\
  \left[ {50} \right] = 5 \\
  \left[ { - 3.010} \right] = - 4 \\
 $
Greatest integer function domain and range-
Domain - The greatest integer function is defined for all real numbers. Hence, as per its definition, its domain is the set of real numbers that are divided into intervals like $\left[ { - 4,3} \right),\left[ { - 3,2} \right)\left[ { - 2,1} \right),\left[ { - 1,0} \right)$ and so on.
Range- Range of the greatest integer function is nothing but all the integers.
Graphical representation of greatest integer function:

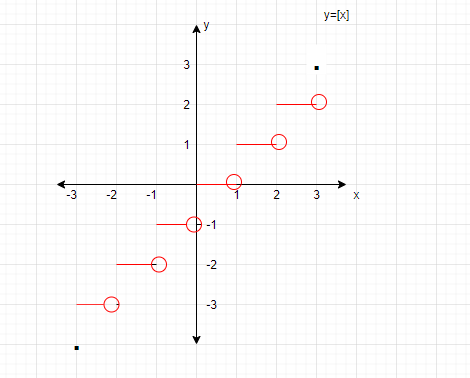
When the intervals are in the form of (n, n+1), the value of greatest integer function is n, where n is an integer.
For example, the greatest integer function of the interval $\left[ {3,4} \right)$ will be 3.
The graph is not continuous. For instance, below is the graph of the function $f\left( x \right) = \left[ x \right]$

The above graph is viewed as a group of steps and hence the integer function is also called a Step function.

Note: In order to solve this question, we will try to interpret all the steps one by one, first define the greatest integer function then also mention some of the examples of greatest integer function and then by defining the domain and range of the greatest integer function and explain it graphically we can easily solve this question.