
Define \[f:\left[ -\dfrac{1}{2},\infty \right)\to R\]by \[f\left( x \right)=\sqrt{1+2x},x\in \left[ -\dfrac{1}{2},\infty \right),\]then compute \[\underset{x\to -{{\dfrac{1}{2}}^{+}}}{\mathop{\lim }}\,f\left( x \right)\]. Hence find \[\underset{x\to -\dfrac{1}{2}}{\mathop{\lim }}\,f\left( x \right)\].
Answer
544.2k+ views
Hint: In order to define the function, we need to find the points of discontinuity of the function, this can be found by putting \[f\left( x \right)=\sqrt{1+2x}\] equal to zero. Then, finding limits of \[f\left( x \right)\] at values of \[x\] slightly greater than \[-\dfrac{1}{2}\] and that at \[-\dfrac{1}{2}\].
Formula used:
In order to draw the graph, the various points are considered and plotted. The domain for the function is \[\left[ -\dfrac{1}{2},\infty \right),\left\{ x\left| x \right.\ge -\dfrac{1}{2} \right\}\] as the interval over which function is defined is given as \[f:\left[ -\dfrac{1}{2},\infty \right)\to R\] in the question.
To find the, \[\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)\]
\[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)\] and \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)\] should exist and coincide.
Complete step by step solution:
Equating \[f\left( x \right)\] to zero will give the roots
\[\sqrt{1+2x}=0\]
Squaring both sides
\[\begin{align}
& 1+2x=0 \\
& x=-\dfrac{1}{2} \\
\end{align}\]
So, the function is discontinuous at the point \[x=-\dfrac{1}{2}\]
If we plot a graph using these points,
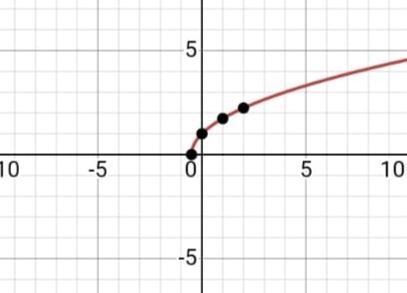
The domain of the function is found by finding where the equation is defined. The range is the set of values that correspond to the domain.
So, the domain is \[\left[ -\dfrac{1}{2},\infty \right),\left\{ x\left| x \right.\ge -\dfrac{1}{2} \right\}\]
And the range is: \[\left[ 0,\infty \right),\left\{ y\left| y \right.\ge 0 \right\}\]
Now, in order to find \[\underset{x\to -{{\dfrac{1}{2}}^{+}}}{\mathop{\lim }}\,f\left( x \right)\]
We solve it in this manner,
\[x\leftrightarrow -\dfrac{1}{2}+h\]
Where \[h\to 0\]
\[\begin{align}
& \Rightarrow \underset{h\to 0}{\mathop{\lim }}\,f\left( -\dfrac{1}{2}+h \right) \\
& \Rightarrow \underset{h\to 0}{\mathop{\lim }}\,\sqrt{1+2\left( -\dfrac{1}{2}+h \right)} \\
& \Rightarrow \underset{h\to 0}{\mathop{\lim }}\,\sqrt{1-1+h} \\
& \Rightarrow 0 \\
\end{align}\]
Now, the range is from\[\left[ -\dfrac{1}{2},\infty \right)\], now as the left hand limit does not lie in the range. The left hand limit does not exist.
Now for \[\underset{x\to -\dfrac{1}{2}}{\mathop{\lim }}\,f\left( x \right)\] to exist, the left hand limit and the right hand limit should coincide. However, it is not so, in this case. So, the limit \[\underset{x\to -\dfrac{1}{2}}{\mathop{\lim }}\,f\left( x \right)\] does not exist.
Note: The function is discontinuous at \[x=-\dfrac{1}{2}\] means that the curve is not continuous at this point or makes a jump or is broken .If the interval contained the values less than \[-\dfrac{1}{2}\], then the left hand limit would have existed and also the \[\underset{x\to -\dfrac{1}{2}}{\mathop{\lim }}\,f\left( x \right)\].
Formula used:
In order to draw the graph, the various points are considered and plotted. The domain for the function is \[\left[ -\dfrac{1}{2},\infty \right),\left\{ x\left| x \right.\ge -\dfrac{1}{2} \right\}\] as the interval over which function is defined is given as \[f:\left[ -\dfrac{1}{2},\infty \right)\to R\] in the question.
To find the, \[\underset{x\to a}{\mathop{\lim }}\,f\left( x \right)\]
\[\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)\] and \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)\] should exist and coincide.
Complete step by step solution:
Equating \[f\left( x \right)\] to zero will give the roots
\[\sqrt{1+2x}=0\]
Squaring both sides
\[\begin{align}
& 1+2x=0 \\
& x=-\dfrac{1}{2} \\
\end{align}\]
So, the function is discontinuous at the point \[x=-\dfrac{1}{2}\]
If we plot a graph using these points,
| x | y |
| -0.5 | 0 |
| 0 | 1 |
| 1 | 1.73 |
| 2 | 2.24 |

The domain of the function is found by finding where the equation is defined. The range is the set of values that correspond to the domain.
So, the domain is \[\left[ -\dfrac{1}{2},\infty \right),\left\{ x\left| x \right.\ge -\dfrac{1}{2} \right\}\]
And the range is: \[\left[ 0,\infty \right),\left\{ y\left| y \right.\ge 0 \right\}\]
Now, in order to find \[\underset{x\to -{{\dfrac{1}{2}}^{+}}}{\mathop{\lim }}\,f\left( x \right)\]
We solve it in this manner,
\[x\leftrightarrow -\dfrac{1}{2}+h\]
Where \[h\to 0\]
\[\begin{align}
& \Rightarrow \underset{h\to 0}{\mathop{\lim }}\,f\left( -\dfrac{1}{2}+h \right) \\
& \Rightarrow \underset{h\to 0}{\mathop{\lim }}\,\sqrt{1+2\left( -\dfrac{1}{2}+h \right)} \\
& \Rightarrow \underset{h\to 0}{\mathop{\lim }}\,\sqrt{1-1+h} \\
& \Rightarrow 0 \\
\end{align}\]
Now, the range is from\[\left[ -\dfrac{1}{2},\infty \right)\], now as the left hand limit does not lie in the range. The left hand limit does not exist.
Now for \[\underset{x\to -\dfrac{1}{2}}{\mathop{\lim }}\,f\left( x \right)\] to exist, the left hand limit and the right hand limit should coincide. However, it is not so, in this case. So, the limit \[\underset{x\to -\dfrac{1}{2}}{\mathop{\lim }}\,f\left( x \right)\] does not exist.
Note: The function is discontinuous at \[x=-\dfrac{1}{2}\] means that the curve is not continuous at this point or makes a jump or is broken .If the interval contained the values less than \[-\dfrac{1}{2}\], then the left hand limit would have existed and also the \[\underset{x\to -\dfrac{1}{2}}{\mathop{\lim }}\,f\left( x \right)\].
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




