Question

Define ellipse as a set of all points in the plane and derive its equation in the standard form as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, $\left( a>b \right)$.

Answer 1

Hint: We start solving the problem by recalling the definition of an ellipse using the locus of the points. We then assume the sum of the constant distance between the point and foci as 2a. We then use the formula of the distance between two points and square on both sides and make necessary arrangements to the equations in terms of the sum of ${{x}^{2}}$ and ${{y}^{2}}$. We then assume ${{a}^{2}}-{{c}^{2}}={{b}^{2}}$ and necessary calculations to complete the desired equation.

Complete step by step answer:
According to the problem, we need to define what is an ellipse and derive the equation of the ellipse in its standard form $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, $\left( a>b \right)$.
We know that the ellipse is defined as the locus of all the points such that the sum of the distances from the point in the locus to the foci is constant, as shown in the figure.

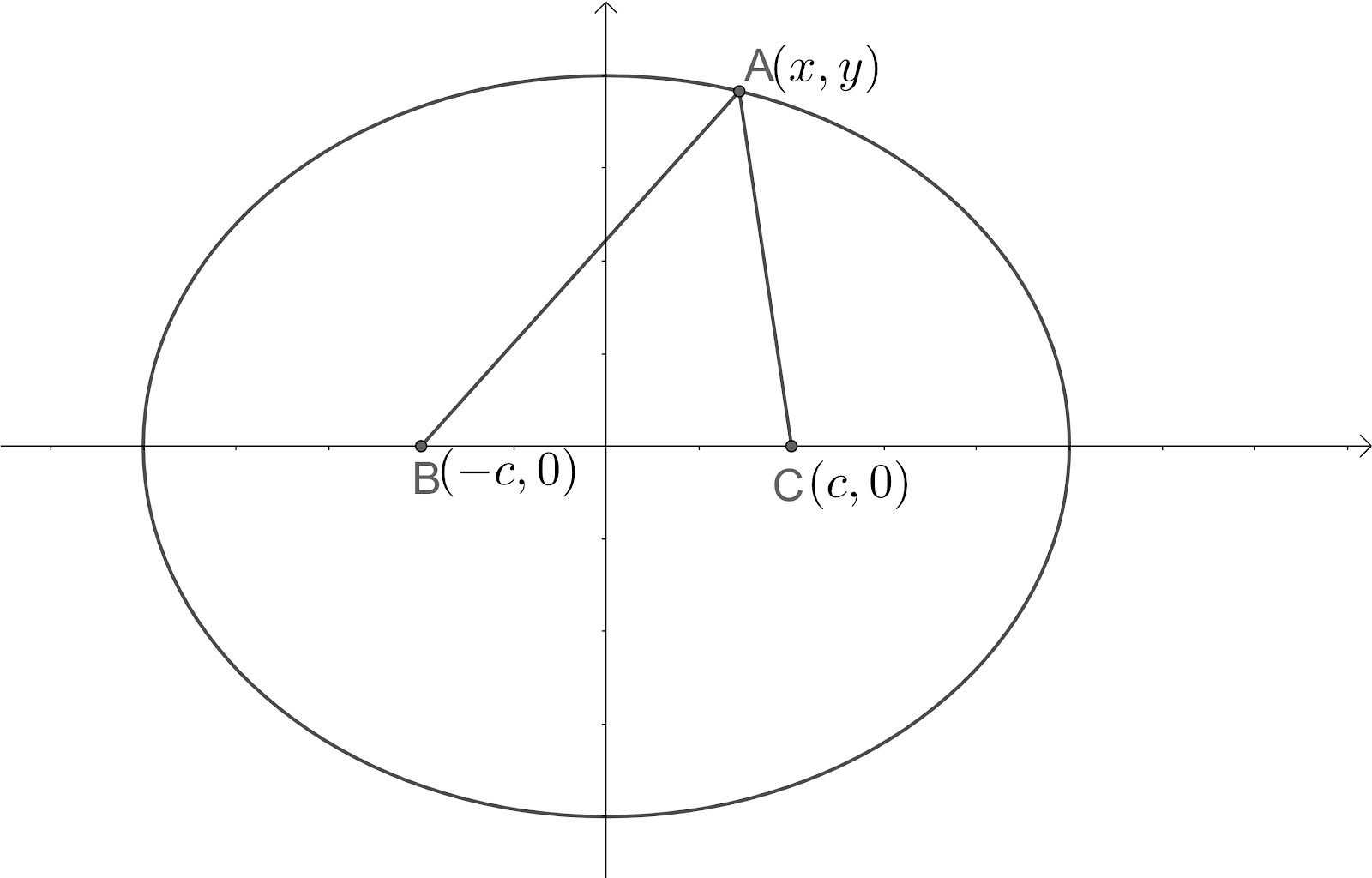
Let us assume the sum of the distances from the focus to the point representing the locus be 2a.
So, we get $AB+AC=2a$.
We know that the distance between the two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$.
So, we have $\sqrt{{{\left( x+c \right)}^{2}}+{{\left( y-0 \right)}^{2}}}+\sqrt{{{\left( x-c \right)}^{2}}+{{\left( y-0 \right)}^{2}}}=2a$.
$\Rightarrow \sqrt{{{\left( x+c \right)}^{2}}+{{y}^{2}}}+\sqrt{{{\left( x-c \right)}^{2}}+{{y}^{2}}}=2a$.
$\Rightarrow \sqrt{{{\left( x+c \right)}^{2}}+{{y}^{2}}}=2a-\sqrt{{{\left( x-c \right)}^{2}}+{{y}^{2}}}$.
Let us square on both sides.
$\Rightarrow {{\left( \sqrt{{{\left( x+c \right)}^{2}}+{{y}^{2}}} \right)}^{2}}={{\left( 2a-\sqrt{{{\left( x-c \right)}^{2}}+{{y}^{2}}} \right)}^{2}}$.
$\Rightarrow {{\left( x+c \right)}^{2}}+{{y}^{2}}=4{{a}^{2}}+{{\left( x-c \right)}^{2}}+{{y}^{2}}-4a\sqrt{{{\left( x-c \right)}^{2}}+{{y}^{2}}}$.
$\Rightarrow {{\left( x+c \right)}^{2}}-{{\left( x-c \right)}^{2}}+{{y}^{2}}-{{y}^{2}}-4{{a}^{2}}=-4a\sqrt{{{\left( x-c \right)}^{2}}+{{y}^{2}}}$.
We know that ${{\left( a+b \right)}^{2}}-{{\left( a-b \right)}^{2}}=4ab$.
$\Rightarrow 4xc-4{{a}^{2}}=-4a\sqrt{{{\left( x-c \right)}^{2}}+{{y}^{2}}}$.
$\Rightarrow xc-{{a}^{2}}=-a\sqrt{{{\left( x-c \right)}^{2}}+{{y}^{2}}}$.
Let us square on both sides.
$\Rightarrow {{\left( xc-{{a}^{2}} \right)}^{2}}={{\left( -a\sqrt{{{\left( x-c \right)}^{2}}+{{y}^{2}}} \right)}^{2}}$.
$\Rightarrow {{x}^{2}}{{c}^{2}}+{{a}^{4}}-2{{a}^{2}}xc={{a}^{2}}\left( {{\left( x-c \right)}^{2}}+{{y}^{2}} \right)$.
$\Rightarrow {{x}^{2}}{{c}^{2}}+{{a}^{4}}-2{{a}^{2}}xc={{a}^{2}}\left( {{x}^{2}}+{{c}^{2}}-2xc+{{y}^{2}} \right)$.
$\Rightarrow {{x}^{2}}{{c}^{2}}+{{a}^{4}}-2{{a}^{2}}xc={{a}^{2}}{{x}^{2}}+{{a}^{2}}{{c}^{2}}-2{{a}^{2}}xc+{{a}^{2}}{{y}^{2}}$.
$\Rightarrow {{a}^{4}}-{{a}^{2}}{{c}^{2}}-2{{a}^{2}}xc-2{{a}^{2}}xc={{a}^{2}}{{x}^{2}}-{{x}^{2}}{{c}^{2}}+{{a}^{2}}{{y}^{2}}$.
$\Rightarrow {{a}^{2}}\left( {{a}^{2}}-{{c}^{2}} \right)={{x}^{2}}\left( {{a}^{2}}-{{c}^{2}} \right)+{{a}^{2}}{{y}^{2}}$.
Let us assume ${{a}^{2}}-{{c}^{2}}={{b}^{2}}$.
$\Rightarrow {{x}^{2}}{{b}^{2}}+{{y}^{2}}{{a}^{2}}={{a}^{2}}{{b}^{2}}$.
Let us divide both sides with ${{a}^{2}}{{b}^{2}}$.
$\Rightarrow \dfrac{{{x}^{2}}{{b}^{2}}}{{{a}^{2}}{{b}^{2}}}+\dfrac{{{y}^{2}}{{a}^{2}}}{{{a}^{2}}{{b}^{2}}}=\dfrac{{{a}^{2}}{{b}^{2}}}{{{a}^{2}}{{b}^{2}}}$.
$\Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.
So, we have found the equation of the ellipse as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.

Note:
Here we have assumed ${{b}^{2}}={{a}^{2}}-{{c}^{2}}$ which tells us the value of a is greater than the value of b. Here we derived the standard equation of the ellipse by assuming origin as centre of the ellipse and x-axis as the major axis and the y-axis as the minor axis of the ellipse. We should not make mistakes while applying the square and calculating the distance between the points. Similarly, we can also expect the problem to derive the equation of parabola and hyperbola