Question

Define coefficient of self-inductance and write its unit.

Answer 1

- Hint: When current flows through a coil, a magnetic field is created in the coil. This magnetic field opposes alternating current to pass through it. Coefficient of self-inductance is related to the induced magnetic field in a coil. Self-inductance is an important property of a coil, utilised in many filtering processes.

Complete step-by-step solution
Self-inductance is the property of a coil by virtue of which, the coil opposes any change in the current flowing through it, by inducing an electromotive force in itself. When current in a coil is changed with the help of a resistor as shown in the diagram, an emf is induced in the coil. This self-induced emf opposes further alternating current to flow through the coil.

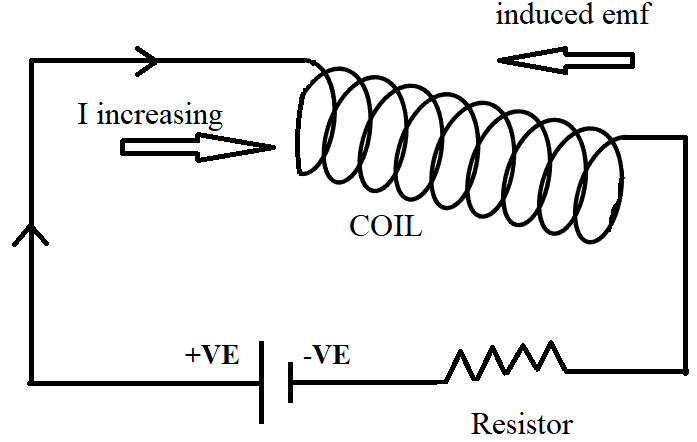
Let a current of strength $I$ flow through a coil and $\phi $ be the magnetic flux induced in the coil. It is found that
$\phi \propto I\Rightarrow \phi =LI$
where
$L$ is the coefficient of self-inductance
The value of $L$depends upon the number of turns, area of cross-section and nature of the material used in the core of the coil, on which the coil is wound.
If unit current flows through a coil, self-inductance is equal to the magnetic flux induced in the coil.
For $I=1$, $\phi =LI=L(1)=L$
Numerically, the coefficient of self-inductance of a coil is equal to the amount of magnetic flux linked with the coil when unit current flows through the coil.
Self-inductance can also be defined in terms of emf induced in a coil. We know that emf induced in a coil is given by a negative rate of change of magnetic flux.
$emf=-\dfrac{d\phi }{dt}$
Let this be equation 1.
Equation 1 can be rewritten as
$emf=-\dfrac{d\phi }{dt}=-\dfrac{d(LI)}{dt}=-L\times \dfrac{dI}{dt}$
If rate of change of current with respect to time is unity, then,
$emf=-L\times \dfrac{dI}{dt}=-L\times 1\Rightarrow L=-emf$
Hence, coefficient of self-inductance can also be defined as the emf induced in a coil, when the rate of change of current is unity.
Inductance is a scalar quantity and the unit of coefficient of self-inductance is $henry(H)$
Coefficient of self-inductance of a coil is said to be $1H$, when a current-change, at the rate of $1A{{s}^{-1}}$, induces an $emf$ of $1V$ in the coil.

Note: Induced $emf$ is dependent on its direction. When current in a coil is increasing in a particular direction, the induced $emf$ has a direction opposite to the direction of current flow. When current in a coil is decreasing in a particular direction, the induced $emf$ has a direction opposing the decrease of current flow. This means that induced $emf$ has the same direction as that of current flow.