Question

Define angle of repose. Deduce its relation with coefficient of limiting friction.

Answer 1

Hint:We know that at a certain point of inclination of the plane of the object, the object starts to just move down the plane. We will draw the diagram showing all the components of the forces b resolving them. After that we will equate.

Complete answer:
In the given question, we are talking about the angle of repose. We are asked to define the term ‘angle of repose’.We are also asked to deduce its relation with the coefficient of limiting friction.

To begin with, let us discuss a bit about the angle of repose.
When we place an object on a plane which is inclined with the horizontal plane at some angle, the object remains at rest, due to its weight and friction. As we increase the angle of the inclination of the inclined plane, the object at some point of time, begins to slide down. The minimum angle which the inclined plane makes with the horizontal plane, when the object resting on it just begins to slide down is called angle of repose.

For better understanding, we draw a diagram.
Here in the diagram, the weight of the object acts downwards. The object is sliding in the downward direction. The angle with the plane of the object makes with the horizontal is. It is the minimum angle at which the object just begins to slide down.

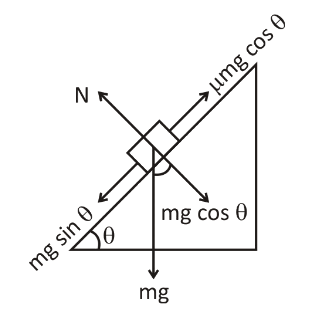
We can now write:
\[mg\sin \theta = \mu N\] …… (1)
Where,
\[\mu \] indicates the coefficient of friction.
\[N\] indicates the normal reaction.
\[\theta \] indicates the angle of repose.

We know:
\[N = mg\cos \theta \] …… (2)
By using the equation (2) in equation (1), we get:
$mg\sin \theta = \mu \times mg\cos \theta \\
\Rightarrow \sin \theta = \mu \cos \theta \\
\Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \mu \\
\Rightarrow \tan \theta = \mu \\$
\[ \therefore \theta = {\tan ^{ - 1}}\mu \]

Hence, we found the relation between the angle of repose with the coefficient of limiting friction.

Note:While solving this problem, it is important to draw the diagram which shows all the forces along with the components. If we fail to show all the resolved forces, we will definitely get irrelevant results. It is important to remember that the normal reaction always acts perpendicular to the plane of the object.