Question

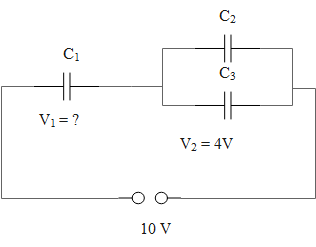
Define a capacitor. Draw a circuit diagram and obtain a relation for equivalent capacitance in the series combination of capacitors. In the given circuit diagram write the value of \[{{V}_{1}}\]

Answer 1

Hint: A capacitor is an electric component used to store charge and energy. The equivalent capacitance of the series combination of the capacitors is the reciprocal of the sum of series of the individual reciprocal values of the capacitance of capacitors. Using the property of the series and parallel combination of capacitors, we will find the capacitance value.
Formula used:
\[C=\dfrac{Q}{V}\]

Complete answer:
An electric component that has the ability to store the electrical energy in form of the charges producing the potential difference is called the capacitor. The capacitance of the capacitor is given as a charge stored by it by the potential difference it produces. The mathematical representation of the same is given as follows.
\[C=\dfrac{Q}{V}\]
The circuit diagram representing the series combination of capacitors is given as follows.

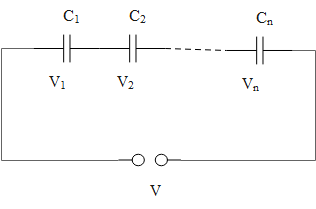
The capacitors are said to be connected in series when the negative plate of one capacitor is connected to the positive plate of the other capacitor and so on. In the case of the series combination of capacitors, the charge across each capacitor remains the same, while the capacitors will have different potential differences across them. So, we have,
\[{{V}_{1}}=\dfrac{Q}{{{C}_{1}}},{{V}_{2}}=\dfrac{Q}{{{C}_{2}}},{{V}_{3}}=\dfrac{Q}{{{C}_{3}}},....,{{V}_{n}}=\dfrac{Q}{{{C}_{n}}}\]
The sum of the potential difference of the individual capacitors equals the equivalent potential difference of the series combination of the capacitors.
\[\begin{align}
  & V={{V}_{1}}+{{V}_{2}}+.....+{{V}_{n}} \\
 & \Rightarrow \dfrac{Q}{C}=\dfrac{Q}{{{C}_{1}}}+\dfrac{Q}{{{C}_{2}}}+.......+\dfrac{Q}{{{C}_{n}}} \\
\end{align}\]
As the charge across the capacitors remains the same, so, take it in common.
 \[\begin{align}
  & \dfrac{Q}{C}=Q\left[ \dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+.......+\dfrac{1}{{{C}_{n}}} \right] \\
 & \therefore \dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+.......+\dfrac{1}{{{C}_{n}}} \\
\end{align}\]
A relation for equivalent capacitance in the series combination of capacitors is,
\[\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+.......+\dfrac{1}{{{C}_{n}}}\]
Consider the circuit diagram.

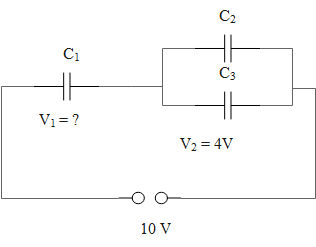
The sum of the potential difference of the individual capacitors equals the equivalent potential difference of the series combination of the capacitors.
\[\begin{align}
  & V={{V}_{1}}+{{V}_{2}} \\
 & \Rightarrow 10={{V}_{1}}+4 \\
 & \therefore {{V}_{1}}=10-4=6\,V \\
\end{align}\]
Therefore, the value of \[{{V}_{1}}\]is 6 V.
\[\therefore \] A capacitor is an electric component used to store charge and energy. A relation for equivalent capacitance in the series combination of capacitors is, \[\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+.......+\dfrac{1}{{{C}_{n}}}\]. The value of \[{{V}_{1}}\] is 6 V.

Note:
The equivalent capacitance of the series combination of capacitors is computed in the same way as the equivalent resistance of the parallel combination of resistors. Similarly, the equivalent capacitance of the parallel combination of capacitors is computed in the same way as the equivalent resistance of the series combination of resistors.