Question

What is the decrease in weight of a body of mass $500\,kg$ when it is taken into a mine of depth $1000\,km$. (Radius of earth, $R = 6400\,km$ , $g = 9.8\,m{s^{ - 2}}$)

Answer 1

Hint: The decrease in the weight of the body can be calculated by subtracting the weight of mass into the mine from the weight of mass from the earth’s surface. For this, we will first calculate the mass and the radius of the mine. Here, we will also calculate the acceleration due to gravity acting on the mass into the mine.

Complete step by step answer:
Consider a mine of depth $1000\,km$ and let a body of mass $500\,kg$ be taken into the depth. Therefore, the mass of the body, $M = 500\,kg = 0.5g$.
Also, the depth of mine, $d = 1000\,km = 1 \times {10^3}m$
Also, radius of earth is given as, $R = 6400\,km = 6.4 \times {10^3}m$
And, the acceleration due to gravity, $g = 9.8\,m{s^{ - 2}}$

The diagram showing the above system is given by;

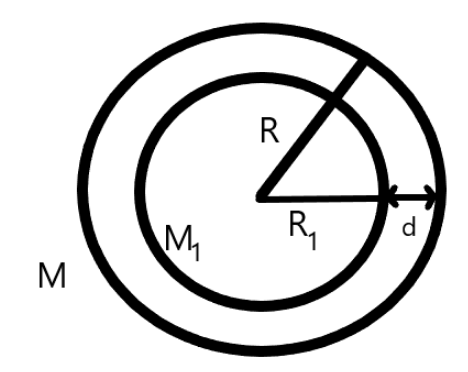
Now, if we want to find the radius ${R_1}$ , we will use the relation according to the figure as shown below
${R_1} = R - d$
$ \Rightarrow \,{R_1} = \left( {6400 - 1000} \right)$
$ \Rightarrow \,{R_1} = 5400\,km$
$ \Rightarrow \,{R_1} = 5.4 \times {10^6}\,m$
Now, we know that the distance $$d$$ is comparable with ${R^3}$ , therefore, we can’t use approximate values. Now, mass ${M_1}$ can be calculated as shown below
${M_1} = \dfrac{M}{{\dfrac{4}{3}\pi {R^3}}} \times 4\pi {R_1}$
$ \Rightarrow {M_1} = \dfrac{{3M}}{{{{\left( {6.4 \times {{10}^3}} \right)}^3}}} \times 5.4 \times {10^6}$
$ \Rightarrow {M_1} = \dfrac{{3M}}{{262.1 \times {{10}^9}}} \times 67.8 \times {10^6}$
$ \Rightarrow {M_1} = 3M \times 0.258 \times {10^{ - 3}}$
$ \Rightarrow \,{M_1} = 0.6 \times {10^{ - 3}} \times M$
$ \Rightarrow \,{M_1} = 0.6M \times {10^{ - 3}}$
Now, using the law of gravitational formula as shown below
$g = \dfrac{{GM}}{{{R^2}}}$
${g_1} = \dfrac{{G{M_1}}}{{R_1^2}}$
Now, dividing ${g_1}$ by $g$ , we get
$\dfrac{{{g_1}}}{g} = \dfrac{{G{M_1}}}{{R_1^2}} \times \dfrac{{{R^2}}}{{GM}}$
$ \Rightarrow \,\dfrac{{{g_1}}}{g} = \dfrac{{{M_1}{R^2}}}{{MR_1^2}}$
$ \Rightarrow \,\dfrac{{{g_1}}}{g} = \dfrac{{0.6M \times {{10}^{ - 3}} \times {{\left( {6.4 \times {{10}^3}} \right)}^2}}}{{M \times \left( {5.4 \times {{10}^6}} \right)}}$
$ \Rightarrow \,\dfrac{{{g_1}}}{g} = \dfrac{{0.6 \times {{10}^{ - 3}} \times 40.9 \times {{10}^6}}}{{29.16 \times {{10}^6}}}$
$ \Rightarrow \,\dfrac{{{g_1}}}{g} = \dfrac{{24.54 \times {{10}^3}}}{{29.16 \times {{10}^6}}}$
$ \Rightarrow \,\dfrac{{{g_1}}}{g} = 0.84 \times {10^{ - 3}}$
$ \Rightarrow \,{g_1} = 0.84 \times 9.8 \times {10^{ - 3}}$
$ \Rightarrow \,{g_1} = 8.2 \times {10^{ - 3}}m{s^{ - 2}}$
Now, the weight on the surface of earth can be the force of gravity and can be defined as the product of mass and gravity as shown below
$w = mg$
$ \Rightarrow \,w = 500 \times 9.8$
$ \Rightarrow \,w = 4900\,N$
Also, the weight of the mass that is hanged into the mine is given below
${w_1} = m{g_1}$
$ \Rightarrow \,w = 500 \times 8.26$
$ \Rightarrow \,w = 4130\,N$
Now, the decrease in the weight is given by
$\Delta w = w - {w_1}$
$ \Rightarrow \,\Delta w = 4900 - 4130$
$ \therefore \,\Delta w = 770\,N$

Therefore, the decrease in the weight of the body is $770\,N$.

Note:For solving these types of questions, always remember to convert larger units into smaller units. Here, we will convert the units of mass and radius of the body before taking it into the mine. Here, the acceleration due to gravity on the mass that is taken into the mine will be different because the mass is taken deep into the surface of earth.