Question

Decomposition of $N{H_4}N{O_2}(aq)$ into ${N_2}(g)$ and $2{H_2}O(l)$ is a first order reaction. Which of the following graphs is correct?

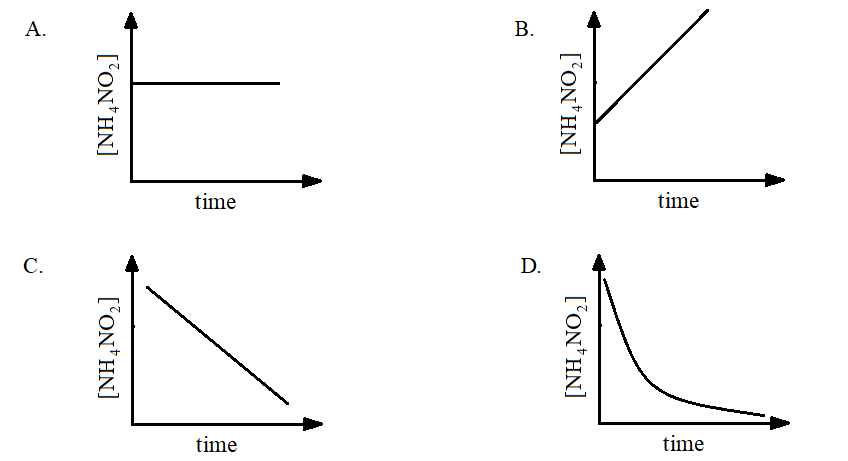
Answer 1

Hint: We know that a rate of reaction is defined as the change in the concentration of the reactants and products per unit time and the first order reaction is the one in which the rate of reaction depends upon the concentration of only one reactant. The given graphs are plotted between the concentration of reactants after time $t$ and time.

Complete answer:
First, we will see how the decomposition reaction proceeds:
$N{H_4}N{O_2} \to {N_2}(g) + 2{H_2}O(l)$
Here the rate of reaction $ = k[N{H_4}N{O_2}]$
Since the power of $[N{H_4}N{O_2}]$ is one therefore this reaction is called the first order reaction.
We know that the expression for the rate constant for the first order reaction is: ${[A]_t} = {[A]_0}{e^{ - kt}}$
Where ${[A]_t} = $ The initial concentration of reactants at $t = 0$
And ${[A]_0} = $ The concentration reactant after $t = t$
So if $'a'$ is the initial concentration of reactant $A$ and $x$ is the amount of reactant getting converted to products in time $t$, then the amount left after time $t$ will be equal to $(a - x)$
hence on substituting the value of ${[A]_0} = a$ and ${[A]_t} = (a - x)$ in ${[A]_t} = {[A]_0}{e^{ - kt}}$ we get:
$k = \dfrac{{2.303}}{t}{\log _{10}}\dfrac{a}{{a - x}}$
so, the graph for the first order reaction plotted between concentration and time will be:

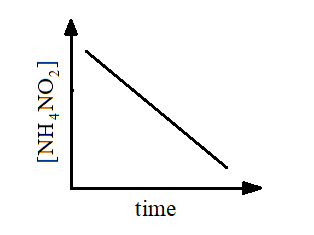
The straight line shows that as the time will increase the concentration will keep on decreasing.
Therefore, the correct answer is Option C.

Note: The slope for the first order reaction is equal to $ - \dfrac{k}{{2.303}}$. The order of reaction is equal to the sum of the exponents to which the concentration terms in the rate law are raised. it may be a fraction, a whole number or even zero and it is always determined by experimental methods.