Question

D, E and F are respectively the midpoints of the sides BC, CA and AB of a \[\Delta ABC\]. Show that:
(i) BDEF is a parallelogram
(ii) \[ar\left( \Delta DEF \right)=\dfrac{1}{4}ar\left( \Delta ABC \right)\]
(iii) \[ar\left( \square BDEF \right)=\dfrac{1}{2}ar\left( \Delta ABC \right)\]

Answer 1

Hint: We are given certain information with respect to a triangle, \[\Delta ABC\]. Based on the given information we have to prove what is asked in the sub parts. For (i) in order to prove that a certain geometry is a parallelogram, we have to show that the opposite sides are parallel. For (ii) we have to show that the triangles formed by joining the midpoint of the sides have the same area and then compute them to prove the given statement. And for (iii), we will make use of the properties of parallelogram and also the (ii) statement which we had proved and we will get the required expression.

Complete step-by-step solution:
According to the given question, we are given that in a \[\Delta ABC\], the points D, E and F are respectively the midpoints of the sides BC, CA and AB. And based on this, we have to prove the sub parts.
We will first draw the figure of the given \[\Delta ABC\] and also specify the mid-points associated.

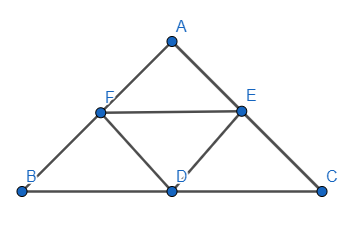
(i) To prove: BDEF is a parallelogram
Proof:
In order to prove that BDEF is a parallelogram, we have to show that the opposite sides are parallel.
We know that F is the midpoint of AB and E is the midpoint of AC and D is the midpoint of BC.
The line EF shows a parallel relationship with respect to the side BC, that is, \[EF||BC\]
This is because we know that in a triangle, the line segment joining the midpoints of two sides of a triangle is parallel to the third side. So, we have,
\[EF||BD\]----(1)
Similarly, we have \[ED||AB\] and which we can write it as,
\[ED||BF\]----(2)
From the equations (1) and (2), we can conclude that the opposite sides of BDEF are parallel. Hence, BDEF is a parallelogram.
(ii) To prove: \[ar\left( \Delta DEF \right)=\dfrac{1}{4}ar\left( \Delta ABC \right)\]
Proof: In the given \[\Delta ABC\], we first have to consider all the parallelograms and each of them is proved using the proof shown in the previous part.
The parallelogram that we have are, \[\square BDEF,\square AFDE,\square FDCE\]
In \[\square BDEF\], FD is the diagonal and we get the two triangles with the equal area, that is,
\[ar\left( \Delta FBD \right)=ar\left( \Delta DEF \right)\]----(1)
Similarly, for parallelograms \[\square AFDE\] and \[\square FDCE\], we have,
\[ar\left( \Delta FAE \right)=ar\left( \Delta DEF \right)\]----(2)
\[ar\left( \Delta DCA \right)=ar\left( \Delta DEF \right)\]----(3)
So, we have in \[\Delta ABC\], four triangles, which we can write it as,
\[ar\left( \Delta ABC \right)=ar\left( \Delta FBD \right)+ar\left( \Delta FAE \right)+ar\left( \Delta DCA \right)+ar\left( \Delta DEF \right)\]
Taking into consideration the equations (1), (2) and (3), we can write the above expression as,
\[\Rightarrow ar\left( \Delta ABC \right)=4ar\left( \Delta DEF \right)\]
Rearranging the above expression, we get,
\[\Rightarrow ar\left( \Delta DEF \right)=\dfrac{1}{4}ar\left( \Delta ABC \right)\]
Hence, proved.
(iii) A diagonal of a parallelogram divides the parallelogram into two equal triangles with the same area.
In \[\square BDEF\], FD is the diagonal and we get the two triangles with the equal area.
\[ar\left( \square BDEF \right)=ar\left( \Delta FBD \right)+ar\left( \Delta DEF \right)\]
We know that, \[ar\left( \Delta FBD \right)=ar\left( \Delta DEF \right)\], so we get,
\[\Rightarrow \,ar\left( \square BDEF \right)=ar\left( \Delta DEF \right)+ar\left( \Delta DEF \right)\]
\[\Rightarrow \,ar\left( \square BDEF \right)=2ar\left( \Delta DEF \right)\]
From the part(ii), we have, \[ar\left( \Delta DEF \right)=\dfrac{1}{4}ar\left( \Delta ABC \right)\]
Substituting the value in the expression, we get,
\[\Rightarrow \,ar\left( \square BDEF \right)=2\left( \dfrac{1}{4}ar\left( \Delta ABC \right) \right)\]
And so we get,
\[\Rightarrow ar\left( \square BDEF \right)=\dfrac{1}{2}ar\left( \Delta ABC \right)\]
Hence, proved.

Note: The properties associated with parallelograms should be known and are crucial while solving questions like these. Also, the parallelograms used should be mentioned prior to using them. In the above solution, since we solved for one of the parallelograms, we used its results to define the other parallelograms.