Question

\[D\], \[E\] and \[F\] are respectively the mid-points of sides \[AB\], \[BC\] and \[CA\] of \[\Delta ABC\]. Find the ratio of the areas of \[\Delta DEF\] and \[\Delta ABC\].

Answer 1

Hint: The given of the question is the relation between the points \[D\], \[E\] and \[F\] with \[\Delta ABC\]. It makes the \[\Delta DEF\] inside of \[\Delta ABC\]. We have to find the ratio of the areas of \[\Delta DEF\] and \[\Delta ABC\]. By using some triangle property we are going to find that ratio.
SSS (Side-Side-Side): If three pairs of sides of two triangles are equal in length, then the triangles are congruent. ASA (Angle-Side-Angle): If two pairs of angles of two triangles are equal in measurement, and the included sides are equal in length, then the triangles are congruent.

Complete step-by-step answer:
It is given that, \[D\], \[E\] and \[F\] are respectively the mid-points of sides \[AB\], \[BC\] and \[CA\] of \[\Delta ABC\].
From the given we have convert the relation into diagram,

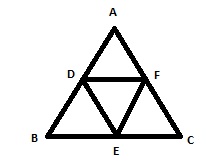
We need to find the ratio of \[\dfrac{{{\text{Area}}(\Delta DEF)}}{{{\text{Area}}(\Delta ABC)}}\].
Since we have to find the ratio of the areas of \[\Delta DEF\] and \[\Delta ABC\], we first need to prove these triangles are similar.
We know that the line joining the mid-points of two sides of a triangle is parallel to the 3rd side.
Now, in \[\Delta ABC\], \[D\], \[E\] and \[F\] are respectively the mid-points of sides \[AB\], \[BC\] and \[CA\] respectively,
\[\therefore DF\parallel BC\]
Also we can write, \[DF\parallel BE \ldots ..\left( 1 \right)\]
Similarly, in \[\Delta ABC\], \[E\] and \[F\] are respectively the mid-points of sides \[BC\] and \[CA\] respectively,
\[\therefore EF\parallel AB\]
Also we can write, \[EF\parallel DB \ldots \ldots \left( 2 \right)\]
From (1) and (2) we have,
\[DF\parallel BE\] and \[EF\parallel DB\]
We know, when opposite sides of a quadrilateral are parallel, the quadrilateral is a parallelogram.
\[\therefore DBEF\] is a parallelogram.
The opposite angles of the parallelogram are equal.
∴\[\angle DBE = \angle DFE\]
We can also write, \[\angle ABC = \angle DFE \ldots ..\left( 3 \right)\]
Similarly we can get, \[DECF\] is a parallelogram.
The opposite angles of the parallelogram are equal.
∴\[\angle ECF = \angle EDF\]
We can also write, \[\angle BCA = \angle EDF \ldots \ldots \ldots \left( 4 \right)\]
Now, in \[\Delta DEF\] and \[\Delta ABC\]
\[\angle ABC = \angle DFE\] [from (3)]
\[\angle BCA = \angle EDF\] [from (4)]
By using AA similarity criteria,
\[ \Rightarrow \Delta DEF \sim \Delta ABC\]
We know that if two triangle are similar,
Ratio of areas is equal to square of ratio of its corresponding sides
\[\dfrac{{{\text{Area}}(\Delta DEF)}}{{{\text{Area}}(\Delta ABC)}} = {\left( {\dfrac{{DE}}{{AC}}} \right)^2}\]
Since \[DECF\] is a parallelogram \[DE = FC\]
\[\dfrac{{{\text{Area}}(\Delta DEF)}}{{{\text{Area}}(\Delta ABC)}} = {\left( {\dfrac{{FC}}{{AC}}} \right)^2}\]
Since \[F\] is the midpoint of \[AC\]
\[\dfrac{{{\text{Area}}(\Delta DEF)}}{{{\text{Area}}(\Delta ABC)}} = {\left( {\dfrac{{\dfrac{1}{2}AC}}{{\dfrac{1}{1}AC}}} \right)^2}\]
Cancelling the common term $AC$ we get,
\[\dfrac{{{\text{Area}}(\Delta DEF)}}{{{\text{Area}}(\Delta ABC)}} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}\]
Hence, the ratio of the areas of \[\Delta DEF\] and \[\Delta ABC\] is \[1:4\].

Note: If an angle of one triangle is congruent to the corresponding angle of another triangle and the lengths of the sides including these angles are in proportion, the triangles are similar. The corresponding sides of similar triangles are in proportion.
We have used the following theorem.
Theorem: If two triangles are similar, then the ratio of the area of both triangles is proportional to the square of the ratio of their corresponding sides.