Question

D and E are points on sides $AB$ and $AC$ respectively of $\Delta ABC$ such that $ar\left( DBC \right)=ar\left( EBC \right)$ . Prove that $DE\parallel BC$ .

Answer 1

Hint: We can solve this type of problem by making use of the properties of triangles. There is a property of triangles which states that if two triangles share the same base and have the same area then they must lie between two same parallel lines. This property can be used to prove that $DE\parallel BC$ .

Complete step by step answer:
A triangle is a 2D figure, that is it can be drawn on a plane. A triangle is a polygon which has three sides. Based on the correlation between the sides, triangles are classified into three groups, which are equilateral, isosceles and scalar.
We are given two points $D$ and $E$ on sides $AB$ and $AC$ of $\Delta ABC$. Also, the area of the two triangles is same i.e., $ar\left( DBC \right)=ar\left( EBC \right)$
We now join the two points D and C and on the other hand we join two points E and B by two line segments.

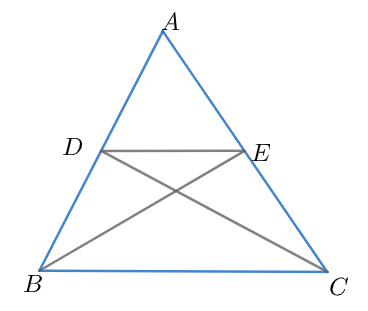
From the above picture we can see that the two triangles $\Delta DBC$ and $\Delta EBC$ share the same base $BC$ . From the properties of triangles, we already know that if two triangles share the same base and have the same area then they must lie between two same parallel lines. This gets us to the point that DE is parallel to BC i.e., $DE\parallel BC$ .
Thus, we have proved the required given.
Note: We can also solve this problem using simple intuition. We are given that the bases and areas of the two triangles are the same. This means that their heights corresponding to those bases must also be the same. This means that D and E are situated at the same height from the base BC, or$DE\parallel BC$ .