
What is the critical value ${{z}_{\dfrac{\alpha }{2}}}$ that corresponds to 93% confidence level?
Answer
524.4k+ views
Hint: We must find the value of $\alpha $ according to the given confidence level of 93%. Then, we can use the definition to get the value of \[P\left( Z>{{z}_{\dfrac{\alpha }{2}}} \right)\] and thus \[P\left( Z<{{z}_{\dfrac{\alpha }{2}}} \right)\]. Then, we can use the z-table to find the corresponding z-score.
Complete step-by-step solution:
We know that using 93% confidence level means that 93% of the times a confidence interval is calculated, it will contain the true value of the parameter.
Also, we know very well that $\alpha $ represents the likelihood that the parameter lies outside the confidence interval.
Here, a confidence level of 93% represents the value 0.93 and so, the value of $\alpha $ will be
$\alpha =1-0.93$.
And thus,
$\alpha =0.07$.
So, we can say that $\dfrac{\alpha }{2}=0.035$.
We know that ${{z}_{\dfrac{\alpha }{2}}}$ is the z-score such that the area under the standard normal curve to the right of ${{z}_{\dfrac{\alpha }{2}}}$ is $\dfrac{\alpha }{2}$.
So, we can write \[P\left( Z>{{z}_{\dfrac{\alpha }{2}}} \right)=0.035\], and so, \[P\left( Z<{{z}_{\dfrac{\alpha }{2}}} \right)=0.965\].
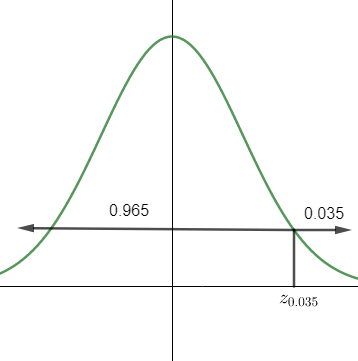
In a z-table having area to the left of z, we must look for the value closest to 0.965 inside the table.
We can see that the value closest to 0.965 is 0.9649, which is present along the row 1.8 and column .01.
Thus, the required z-score is 1.81
Hence, the critical value ${{z}_{\dfrac{\alpha }{2}}}$ for 93% confidence level is 1.81
Note: We can also use the linear interpolation technique to solve this problem. The closest value in the z-table, that is, 0.9649 has z-score 1.81 and 0.9656 has z-score 1.82. So, we can now use linear interpolation to find the value of z-score for 0.965 accurately. But, we must understand that this is the approximate answer only.
Complete step-by-step solution:
We know that using 93% confidence level means that 93% of the times a confidence interval is calculated, it will contain the true value of the parameter.
Also, we know very well that $\alpha $ represents the likelihood that the parameter lies outside the confidence interval.
Here, a confidence level of 93% represents the value 0.93 and so, the value of $\alpha $ will be
$\alpha =1-0.93$.
And thus,
$\alpha =0.07$.
So, we can say that $\dfrac{\alpha }{2}=0.035$.
We know that ${{z}_{\dfrac{\alpha }{2}}}$ is the z-score such that the area under the standard normal curve to the right of ${{z}_{\dfrac{\alpha }{2}}}$ is $\dfrac{\alpha }{2}$.
So, we can write \[P\left( Z>{{z}_{\dfrac{\alpha }{2}}} \right)=0.035\], and so, \[P\left( Z<{{z}_{\dfrac{\alpha }{2}}} \right)=0.965\].

In a z-table having area to the left of z, we must look for the value closest to 0.965 inside the table.
| z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
| 1.7 | .9554 | .9564 | .9573 | .9582 | .9591 | .09599 | .9608 | .9616 | .9625 | .9633 |
| 1.8 | .9641 | .9649 | .9656 | .9664 | .9671 | .9678 | .9686 | .9693 | .9699 | .9706 |
| 1.9 | .9713 | .9719 | .9726 | .9732 | .9738 | .9744 | .9750 | .9756 | .9761 | .9767 |
We can see that the value closest to 0.965 is 0.9649, which is present along the row 1.8 and column .01.
Thus, the required z-score is 1.81
Hence, the critical value ${{z}_{\dfrac{\alpha }{2}}}$ for 93% confidence level is 1.81
Note: We can also use the linear interpolation technique to solve this problem. The closest value in the z-table, that is, 0.9649 has z-score 1.81 and 0.9656 has z-score 1.82. So, we can now use linear interpolation to find the value of z-score for 0.965 accurately. But, we must understand that this is the approximate answer only.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




