Question

Corresponding angles are on the _________ side of the transversal.

Answer 1

Hint: We need to find whether corresponding angles are on the same side of transversal or on the opposite side. We will first see what are corresponding angles and then draw a diagram and try to figure out whether they are on the same side of the transversal or on opposite sides. We will try to distinguish the left and right side by using different colours and then find out whether corresponding angles are of the same colour or different colour. If they are of same colour, they lie on the same side and if they are of different colour, they lie on the opposite side of the transversal.

Complete answer:
First of all, we shall discuss what corresponding angles are? When two parallel lines are drawn and they are intersected by a transversal line, then the angles which are formed in the corresponding corners with the transversal line and the two lines respectively. Let us understand it clearly using a diagram.

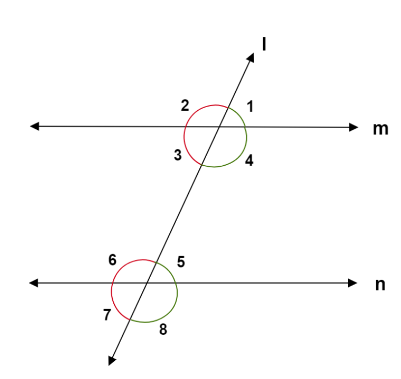
In the above diagram ,we see that m and n are two parallel lines intersected by the transversal l. Now, angles formed by the parallel lines and the transversal are numbered from \[1 - 8\]. Now, we see that \[\angle 1\] and \[\angle 5\] are formed in the same corner i.e. the upper right corner with the transversal line and line m and the transversal and line n respectively.

So, \[\angle 1\] and \[\angle 5\] form a pair of corresponding angles. Similarly, we see that \[\angle 2\] and \[\angle 6\] are formed on the upper left corner of both the lines with the transversal. So, \[\angle 2\] and \[\angle 6\] form a pair of corresponding angles. We also notice that \[\angle 3\] and \[\angle 7\] are formed on the lower left corner of both the lines with the transversal. So, \[\angle 3\] and \[\angle 7\] form a pair of corresponding angles.

At last, we see that \[\angle 4\] and \[\angle 8\] are formed on the lower right corner of the parallel lines. Hence, \[\angle 4\] and \[\angle 8\] form another pair of corresponding angles. Corresponding angles between two parallel lines are equal in measure. Hence, we see that corresponding angles are formed on the same side of the transversal.

Hence, Corresponding angles are on the same side of the transversal.

Note: We should read carefully the definition of corresponding angles. If the definition is misunderstood, we will not be able to identify what are corresponding angles. We need to keep in mind that corresponding angles not only exist between the parallel lines but also the non-parallel lines. It's just that their measure is not equal when the lines are not parallel and equal measure if the lines are parallel.