Question

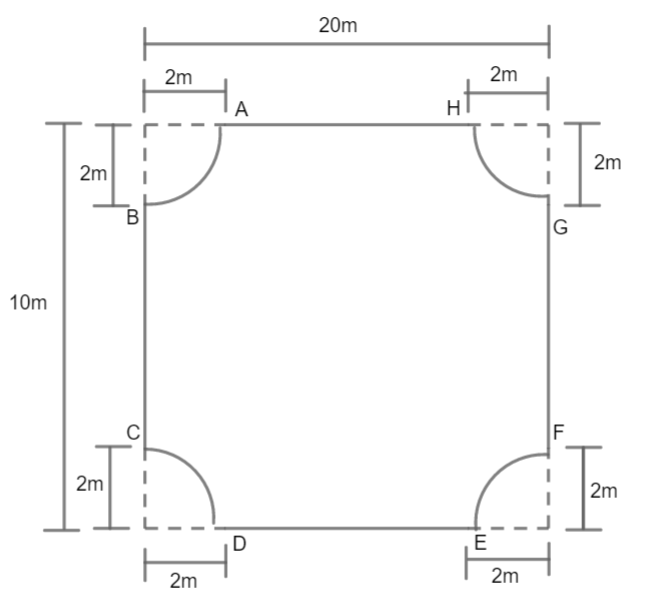
Correct the perimeter of the figure given to one decimal place.

\[\begin{align}
  & A.56.0m \\
 & B.56.6m \\
 & C.57.2m \\
 & D.57.9m \\
\end{align}\]

Answer 1

Hint: In this question, we need to find the perimeter of the given figure which means we need to calculate the length of the boundary of the figure. Corners are in the form of a quarter circle so we will find the circumference of ${{\dfrac{1}{4}}^{th}}$ of a circle and then find the perimeter of such four quarter circles. For the sides, we will subtract extra radius and then find the length of the sides. Adding all length will give us the required perimeter. Circumference of a circle of radius r is given by $2\pi r$.

Complete step by step answer:
We need to find the length of the boundary of the figure, so let us first find the length of the four corners in the figure. As we can see, all corners are in the form of a quarter circle. So let us find the circumference of a quarter circle for finding the length of one corner. Circumference of a circle of radius r is given by $2\pi r$. So, the circumference of the quarter circle of radius r will be $\dfrac{1}{4}\times 2\pi r=\dfrac{1}{2}\pi r$.
Now, for each corner, we can see from the figure that, radius = 2m. Therefore, circumference of one quarter circle $\Rightarrow \left( \dfrac{1}{2}\times \pi \times 2 \right)cm=\pi cm$.
For four corners, perimeter/circumference becomes $\left( 4\times \pi \right)cm=4\pi cm$.
Now let us find the length of the side of the figure.
We are given a total length of horizontal side as 20m but we need length of Ar and DE only. So subtracting extra length we get:
Length of AB $\Rightarrow 20m-\left( 2+2 \right)m=20m-4m=16m$.
Similarly, length DE = 16m.
For vertical sides, we are given length as 10m but we need the length of BC and GF only. So removing extra length we get:
Length of BC $\Rightarrow 10m-\left( 2+2 \right)m=10m-4m=6m$.
Similarly, length of GF = 6m.
So our required perimeter will be the perimeter of four corners + length of four sides.
Therefore, $\text{Perimeter}=\left( 4\pi +16+16+6+6 \right)m=\left( 44+4\pi \right)m$.
As we know $\pi =\dfrac{22}{7}$ so we get: $\Rightarrow \left( 44+\dfrac{88}{7} \right)m$.
Taking LCM of 7 we get: $\Rightarrow \left( \dfrac{308+88}{7} \right)m=56.57m\simeq 56.6m$.
Hence the required perimeter is 56.6m.

So, the correct answer is “Option B”.

Note: Students may forget to subtract two from both ends while finding the length of the side. Since all four corners are part of a circle with radius 2 so 4 corners will make a full circle and hence circumference is simply $2\pi r=2\times 2\times \pi =4\pi $. Make sure to use units of perimeter as meters only.