Question

Copy the figure with punched holes and find the axes of symmetry for the following.

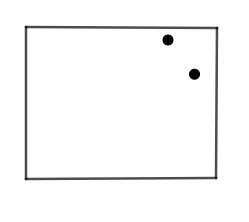
Answer 1

Hint: First of all name the vertices of the given square. Then as we can see that the two dots are mirror images of each other so we can draw a line which will act as a mirror along which the two dots will reflect each other.

Complete step-by-step answer:
The below figure contains a square ABCD along with two dots G and G’.

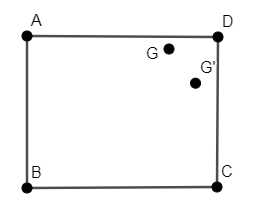
We have to find the axes of symmetry in the above figure. As we can see from the above figure, the two dots G and G’ look like they are mirror images of each other with the mirror passing through the diagonal DB of a square ABCD.
In the below figure, we have drawn a dotted line passing through DB.

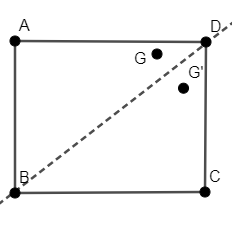
If we carefully see the figure, we will find that DB is acting as a mirror along which dot G’ is the reflection of dot G and vice versa. As we can see that this dotted line is acting as an axis of symmetry because this axis symmetrically divides the whole figure into two parts.
Hence, the dotted line DB is the axis of symmetry of the given figure.

Note: You might think of drawing the axis of symmetry along the diagonal AC but then it won’t divide the whole figure into two equal parts.
Suppose we have drawn the dotted line passing through AC then the figure will look like:

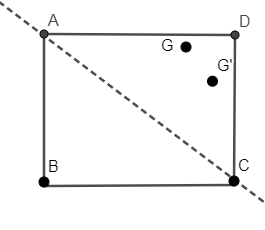
As you can clearly see from the above figure, AC cannot be an axis of symmetry because though square ABCD is divided into two parts but the two dots G and G’ are not reflected along AC.