Question

Copper of fixed volume ‘V’ is drawn into wires of length ‘L’. When this wire is subjected to a constant force ‘F’, the extension produced in the wire is ‘$\Delta l'$ .Which of the following graphs is a straight line?
(A ) $\Delta l$ vs 1/l
(B) $\Delta l$ vs $l^2$
(C) $\Delta l$ vs 1/$l^2$
(D) $\Delta l$ vs l

Answer 1

Hint:The mechanical properties of materials to measure stiffness of the solid materials is known as the Young’s modulus.

Formula used: To solve this type of question we use the following formula.
$Y = \dfrac{{Fl}}{{A\Delta l}}$ ; This is the formula for young’s modulus. Where, F is the force, l is the original length, $\Delta l$ is changed in length and A is the area.

Complete step-by-step answer:
Volume V is given in the question. This can be written in terms of area and length as below.
 V=Al (1)
Let us use Young's modulus formula $Y = \dfrac{{Fl}}{{A\Delta l}}$ and find the expression for change in length.
$Y = \dfrac{{Fl}}{{A\Delta l}}$
$ \Rightarrow \Delta l = \dfrac{{Fl}}{{AY}}$
Now let us substitute the value of area from equation (1).
$\Delta l = \dfrac{{F{l^2}}}{{VY}}$
Let us now, consider all other variables to be constant and find the dependency of $\Delta l$ with length of wire.
$\Delta l \propto {l^2}$

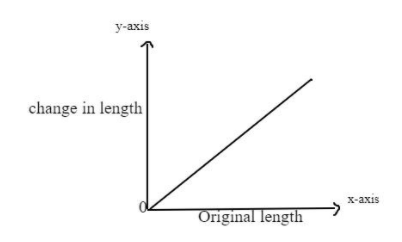
If we plot the graph between the original length that is l versus the change in length $\Delta l$the graph will be a straight-line graph
Hence, option (B) $\Delta l \propto {l^2}$ is the correct option.

Note:
*Young’s modulus is defined as the ratio of stress along an axis to strain along the same axis.
*Young's modulus is a mechanical property that measures the stiffness of solid material and it can be varied concerning the temperature.
*Young's modulus is not always the same in the direction of all materials.
*When stress and strain are nearly zero, the stress-strain curve is linear.
*The relationship between stress and strain is described by Hooke's law that states stress is proportional to strain and the coefficient of proportionality is Young's modulus.
*The higher the young’s modulus, the more stress is needed to create the same amount of strain.
*Young’s modulus is the ability of a material to withstand any changes under lengthwise.