Question

How do you convert \[{{x}^{2}}-{{y}^{2}}=5\] in polar form?

Answer 1

Hint: This question is from the topic of polar system. For solving this question, we should know the relations between x and y with the term r. First, we will know the relations between them. After that we convert the equation in polar form.

Complete step by step answer:
Let us solve this question.
In this question, we have asked to find the conversion of the term \[{{x}^{2}}-{{y}^{2}}=5\] into polar form.
So, for the polar form we can see the below figure.

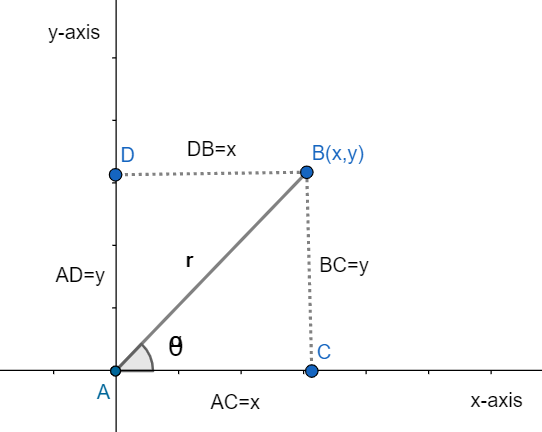
The relations we can see are \[y=r\sin \theta \] and \[x=r\cos \theta \]
So, after putting the values of x and y we can write in the equation \[{{x}^{2}}-{{y}^{2}}=5\] as
\[{{\left( r\cos \theta \right)}^{2}}-{{\left( r\sin \theta \right)}^{2}}=5\]
The above equation can also be written as
\[\Rightarrow {{r}^{2}}{{\cos }^{2}}\theta -{{r}^{2}}{{\sin }^{2}}\theta =5\]
We can take \[{{r}^{2}}\] as common from the left side of the above equation. Hence, we will get
\[\Rightarrow {{r}^{2}}\left( {{\cos }^{2}}\theta -{{\sin }^{2}}\theta \right)=5\]
We are going to use a formula here in the above equation. The formula is \[\cos 2\theta ={{\cos }^{2}}\theta -{{\sin }^{2}}\theta \].
Hence, we can write the above equation as
\[\Rightarrow {{r}^{2}}\left( \cos 2\theta \right)=5\]
We can write the above equation as
\[\Rightarrow {{r}^{2}}=\dfrac{5}{\cos 2\theta }\]
Taking square roots on both sides of the equation, we get
\[\Rightarrow r=\sqrt{\dfrac{5}{\cos 2\theta }}\]

Hence, the conversion of \[{{x}^{2}}-{{y}^{2}}=5\] in polar form will be \[r=\sqrt{\dfrac{5}{\cos 2\theta }}\].

Note: For solving this type of question, we should know how to convert Cartesian form to polar form. Always remember that in polar form, we have only two variables which are r and \[\theta \] (theta). And in Cartesian form we have only two variables which are x and y. The relation between them is given below:
\[y=r\sin \theta \] and \[x=r\cos \theta \].
We should know some formulas of trigonometry. They are very useful in various types of questions. One formula of trigonometry we have used here is \[\cos 2\theta ={{\cos }^{2}}\theta -{{\sin }^{2}}\theta \]. So, don’t forget the formulas of trigonometry.