
How do you convert \[r=1+2\sin \theta \] to rectangular form?
Answer
559.5k+ views
Hint: In this question, we have to convert the polar form into the rectangular form. The given polar form is \[r=1+2\sin \theta \]. In solving this question, first we will get to know through the figure what polar and rectangular form is. After using formulas and doing some process, we will get to convert the equation in rectangular form.
Complete answer:
Let us solve this question.
This question is asked us to convert the polar form into the rectangular form which is given in the question that polar form is \[r=1+2\sin \theta \].
Let us convert the equation \[r=1+2\sin \theta \] in polar form.
First, let us first understand how to convert polar form into rectangular form and vice-versa.
Let us understand this from the given below figure.
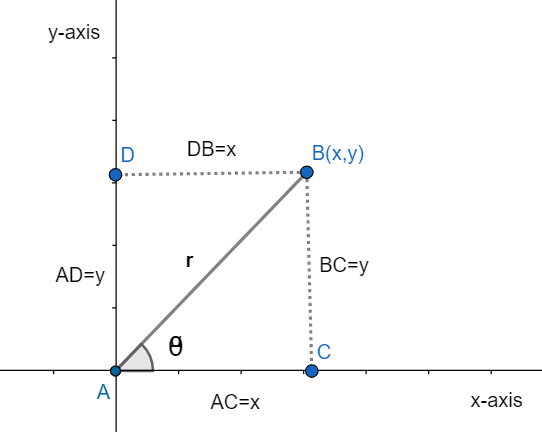
In the above figure, \[\theta \] is the angle between the given line AB and the x-axis. And let the distance between AB is r that is AB=r. Let,
Here, rectangular coordinates are x and y and polar coordinates are r and \[\theta \].
So, we can write from the figure that
\[y=r\sin \theta \] and \[x=r\cos \theta \]
And also we can say that
\[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\]
\[\Rightarrow r=\sqrt{{{x}^{2}}+{{y}^{2}}}\]
So, we have to convert \[r=1+2\sin \theta \] in rectangular form.
Using the above formulas and equations, let us convert the equation in rectangular form.
\[r=1+2\sin \theta \]
Multiply both sides of the equation by r, we get
\[\Rightarrow {{r}^{2}}=r+2r\sin \theta \]
As we know that \[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\] or we can say \[r=\sqrt{{{x}^{2}}+{{y}^{2}}}\]. By using this in the above equation, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}+2\sqrt{{{x}^{2}}+{{y}^{2}}}\sin \theta \]
Taking \[\sqrt{{{x}^{2}}+{{y}^{2}}}\] common in the right side of the equation, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}\left( 1+2\sin \theta \right)\]
And we know that
\[y=r\sin \theta \] or we can say \[\sin \theta =\dfrac{y}{r}\]. After using this formula in the above equation, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}\left( 1+2\times \dfrac{y}{r} \right)\]
Using the formula\[r=\sqrt{{{x}^{2}}+{{y}^{2}}}\], we can write
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}\left( 1+\dfrac{2y}{\sqrt{{{x}^{2}}+{{y}^{2}}}} \right)\]
The above equation can also be written as
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}+2y\]
Taking 2y to the left side of the equation, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2y=\sqrt{{{x}^{2}}+{{y}^{2}}}\]
Now, squaring both sides, we get
\[\Rightarrow {{\left( {{x}^{2}}+{{y}^{2}}-2y \right)}^{2}}={{x}^{2}}+{{y}^{2}}\]
Note: This question belongs to the topic of the polar system from the trigonometric chapter. We should have better knowledge in that for solving this type of question. And also remember the formulas and techniques to convert polar form to rectangular form or vice-versa. Remember the following formulas for the following to solve this type of questions easily.
\[y=r\sin \theta \] ,
\[x=r\cos \theta \], and
\[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\]
Complete answer:
Let us solve this question.
This question is asked us to convert the polar form into the rectangular form which is given in the question that polar form is \[r=1+2\sin \theta \].
Let us convert the equation \[r=1+2\sin \theta \] in polar form.
First, let us first understand how to convert polar form into rectangular form and vice-versa.
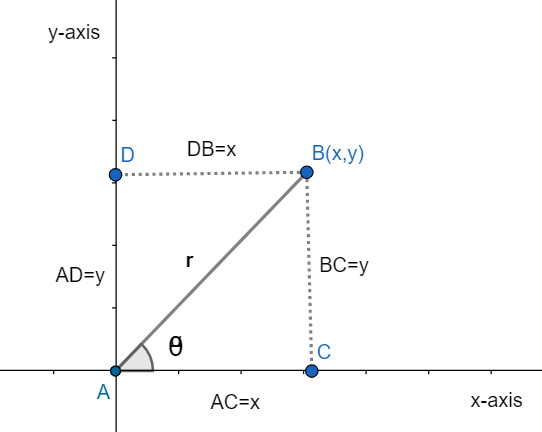
Let us understand this from the given below figure.

In the above figure, \[\theta \] is the angle between the given line AB and the x-axis. And let the distance between AB is r that is AB=r. Let,
Here, rectangular coordinates are x and y and polar coordinates are r and \[\theta \].
So, we can write from the figure that
\[y=r\sin \theta \] and \[x=r\cos \theta \]
And also we can say that
\[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\]
\[\Rightarrow r=\sqrt{{{x}^{2}}+{{y}^{2}}}\]
So, we have to convert \[r=1+2\sin \theta \] in rectangular form.
Using the above formulas and equations, let us convert the equation in rectangular form.
\[r=1+2\sin \theta \]
Multiply both sides of the equation by r, we get
\[\Rightarrow {{r}^{2}}=r+2r\sin \theta \]
As we know that \[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\] or we can say \[r=\sqrt{{{x}^{2}}+{{y}^{2}}}\]. By using this in the above equation, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}+2\sqrt{{{x}^{2}}+{{y}^{2}}}\sin \theta \]
Taking \[\sqrt{{{x}^{2}}+{{y}^{2}}}\] common in the right side of the equation, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}\left( 1+2\sin \theta \right)\]
And we know that
\[y=r\sin \theta \] or we can say \[\sin \theta =\dfrac{y}{r}\]. After using this formula in the above equation, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}\left( 1+2\times \dfrac{y}{r} \right)\]
Using the formula\[r=\sqrt{{{x}^{2}}+{{y}^{2}}}\], we can write
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}\left( 1+\dfrac{2y}{\sqrt{{{x}^{2}}+{{y}^{2}}}} \right)\]
The above equation can also be written as
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{{{x}^{2}}+{{y}^{2}}}+2y\]
Taking 2y to the left side of the equation, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2y=\sqrt{{{x}^{2}}+{{y}^{2}}}\]
Now, squaring both sides, we get
\[\Rightarrow {{\left( {{x}^{2}}+{{y}^{2}}-2y \right)}^{2}}={{x}^{2}}+{{y}^{2}}\]
Note: This question belongs to the topic of the polar system from the trigonometric chapter. We should have better knowledge in that for solving this type of question. And also remember the formulas and techniques to convert polar form to rectangular form or vice-versa. Remember the following formulas for the following to solve this type of questions easily.
\[y=r\sin \theta \] ,
\[x=r\cos \theta \], and
\[{{x}^{2}}+{{y}^{2}}={{r}^{2}}\]

Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




