Question

Convert r = 4sinθ to its rectangular form.

Answer 1

Hint:As we can see in the question, the equation is given in the polar form and we need to change that into rectangular form. For that use the conversion formulas from polar to rectangular form, \[{r^2} = {x^2} + {y^2}\] and tan θ = $\dfrac{y}{x}$. Also, the equation in the question contains a sine function, whereas the formula contains a tan function. Convert the tan function to a sine function and proceed for the answer.

Complete step by step solution:
The general equation to circles passing through r = 0, with radius
'a' and the centre at polar (a, α) is r = 2a cos(θ−α).

Compared with the general equation above, r = 4sinθ is an equation of a circle of diameter of 4 units and the centre of the circle is at (2, \[\dfrac{\pi }{2}\]).

To convert the equation of the circle to its cartesian form, we have sin θ = $\dfrac{y}{r}$ ….. …. (i) and \[{r^2} = {x^2} + {y^2}\]……. …(ii)

Substituting the values, we get
 r = 4 ($\dfrac{y}{r}$)
$ \Rightarrow {r^2} = 4y$…….(iii)

At the pole we have r= θ = 0, and so, x = y = 0.

Next putting values of equation (ii) in equation (iii),
${r^2} = {x^2} + {y^2} = 4y$

In the standard form,
${x^2} + {y^2} = {2^2}$

Note:

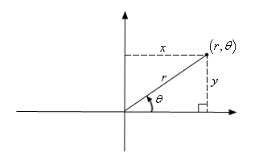
The above figure is the origin of the general formulas used for conversion of polar coordinates into
rectangular coordinates and vice-versa. You can clearly see that tan θ= $\dfrac{y}{x}$ and from
By Pythagoras theorem we also have \[{r^2} = {x^2} + {y^2}\].