Question

How do you convert r = 3 in rectangular form?

Answer 1

Hint: We will first find r in terms of x and y. Then we will have a circle with centre as origin. We can draw the circle and join the x – coordinate at the line to x – axis and similarly y – axis.

Complete step by step solution:
We are given that we are required to convert r = 3 in the rectangular form.
Since, we know that in polar form, ${r^2} = {x^2} + {y^2}$.
Taking the square – root of the above equation on both the sides, we will then obtain the following equation:-
$ \Rightarrow r = \sqrt {{x^2} + {y^2}} $
Putting this in the given equation r = 3, we will then obtain the following equation as:-
$ \Rightarrow \sqrt {{x^2} + {y^2}} = 3$
Taking the square of the above equation on both the sides, we will then obtain the following equation:-
$ \Rightarrow {x^2} + {y^2} = {3^2}$
Simplifying the calculations on the right hand side of the above equation, we will then obtain the following equation with us:-
$ \Rightarrow {x^2} + {y^2} = 9$
Plotting this circle on the axis, we will then obtain the following equation as:-

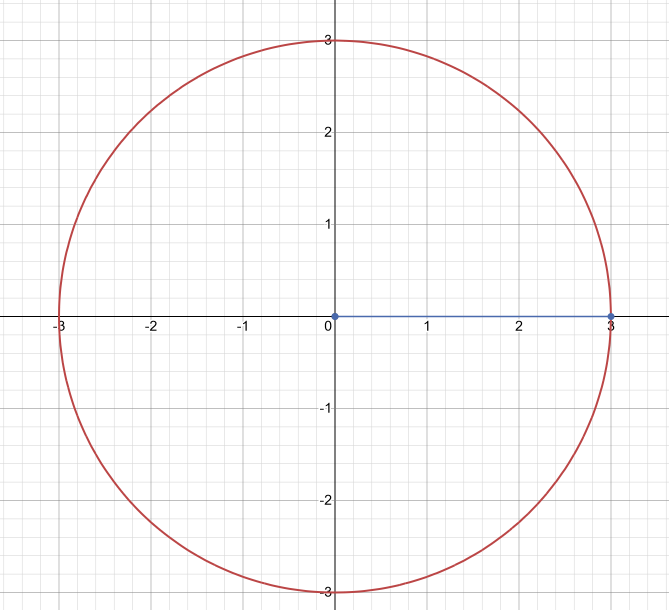
Now, if we wish to convert this in rectangular form, we will then get the following image:-

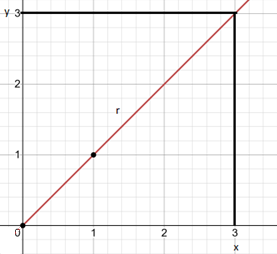
Thus, we have the required answer.

Note: The students must note that in the rectangular form, we just took the point on the circle and joined it to both the x and y – axis to get the rectangular form.
The students must know that in polar form, we assume that:
$ \Rightarrow x = r\cos \theta $
$ \Rightarrow y = r\sin \theta $
Squaring both the above equations on both the sides, we will then obtain the following equations:-
$ \Rightarrow {x^2} = {r^2}{\cos ^2}\theta $
$ \Rightarrow {y^2} = {r^2}{\sin ^2}\theta $
Adding both the above equations, we will then obtain the following equation as:-
$ \Rightarrow {x^2} + {y^2} = {r^2}{\cos ^2}\theta + {r^2}{\sin ^2}\theta $
Taking ${r^2}$ common from both the terms in the right hand side, we will then obtain the following equation as:-
$ \Rightarrow {x^2} + {y^2} = {r^2}\left( {{{\cos }^2}\theta + {{\sin }^2}\theta } \right)$
Since, we know that we have an identity which states that: ${\cos ^2}\theta + {\sin ^2}\theta = 1$. Thus, we have:-
$ \Rightarrow {x^2} + {y^2} = {r^2} \times 1$
Simplifying the calculations on the right hand side in the above equation, we will then obtain the following equation:-
$ \Rightarrow {x^2} + {y^2} = {r^2}$