
How do you convert $\left( -2,0 \right)$from Cartesian to polar coordinates? \[\]
Answer
557.7k+ views
Hint: We recall the definitions of the polar coordinates $\left( r,\theta \right)$and Cartesian coordinates$\left( x,y \right)$. We find $r$ as the distance between origin and the Cartesian point as $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$ and $\theta $ as the angle the ray joining the origin and the point makes with positive $x-$axis $\theta =\operatorname{atan}2\theta $ where $\operatorname{atan}2\left( y,x \right)$ represents 2-argument inverse tangent function.\[\]
Complete step by step answer:
We know that Cartesian coordinate system the position of the any point on the plane is represented by an ordered pair $\left( x,y \right)$ where the real numbers $x,y$ are the distances from perpendicular reference lines called $x-$axis and $y-$axis. The first number is $x$ is called $x-$coordinate measured whose absolute value is distance from $y-$axis and second number $y$ is called $y-$coordinate whose absolute value is distance from $x-$axis.\[\]
We also know that in the polar coordinate system every point is represented in the plane with an ordered pair $\left( r,\theta \right)$ where $r$ is the distance from a reference point (conventionally origin) and $\theta $ is the angle from a reference direction (conventionally positive direction of $x-$axis) . The reference point is called the pole and the reference direction is called the polar axis. Here $r$ is called radial coordinate which is always positive and $\theta \in \left[ 0,2\pi \right)$ is called angular coordinate. \[\]
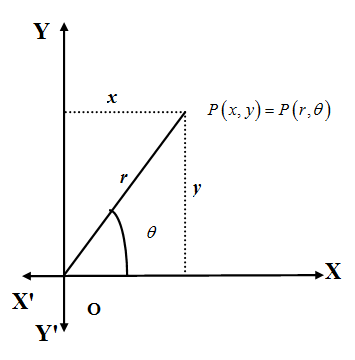
We can convert the Cartesian coordinate $\left( x,y \right)$ to polar coordinate $\left( r,\theta \right)$ of a point using the following relations
\[\begin{align}
& r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
& \theta =\operatorname{atan}2\left( y,x \right) \\
\end{align}\]
The function $\operatorname{atan}2\left( y,x \right)$ called 2-argument inverse tangent is defined as follows;
\[\theta =\left\{ \begin{matrix}
{{\tan }^{-1}}\left( \dfrac{y}{x} \right) & \text{if }x>0 \\
{{\tan }^{-1}}\left( \dfrac{y}{x} \right)+\pi & \text{if }x<0\text{ and }y\ge 0 \\
{{\tan }^{-1}}\left( \dfrac{y}{x} \right)-\pi & \text{if }x<0\text{ and }y<0 \\
\dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\
-\dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\
\text{undefined} & \text{if }x=0\text{ and }y=0 \\
\end{matrix} \right.\]
We are asked to convert $\left( -2,0 \right)=\left( x,y \right)$ which in Cartesian form to polar form. So we have the radial coordinate as
\[r=\sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{{{\left( -2 \right)}^{2}}+0}=\sqrt{4}=2\]
We see that in $\left( -2,0 \right)$ we have $x < 0,y\ge 0$.We find the angular coordinate is using the definition of 2-argument inverse tangent function as
\[\operatorname{atan}2\left( \left( -2,0 \right) \right)=\pi +{{\tan }^{-1}}\left( \dfrac{0}{-2} \right)=\pi +{{\tan }^{-1}}\left( 0 \right)=\pi +0=\pi \]
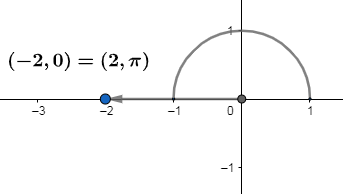
So the polar form of $\left( -2,0 \right)$ is $\left( 2,\pi \right)$ which is drawn below. \[\]
Note: We can convert back from polar coordinate $\left( r,\theta \right)$ to Cartesian coordinate $\left( x,y \right)$ using the conversion formula $x=r\cos \theta ,y=r\sin \theta $. We can alternatively find the polar angle $\theta $ as $\theta ={{\sin }^{-1}}\left( \dfrac{x}{r} \right)$. We note that the radial coordinate is always in radian. We also note that negative numbers are not used to represent polar coordinates unlike Cartesian coordinates.
Complete step by step answer:
We know that Cartesian coordinate system the position of the any point on the plane is represented by an ordered pair $\left( x,y \right)$ where the real numbers $x,y$ are the distances from perpendicular reference lines called $x-$axis and $y-$axis. The first number is $x$ is called $x-$coordinate measured whose absolute value is distance from $y-$axis and second number $y$ is called $y-$coordinate whose absolute value is distance from $x-$axis.\[\]
We also know that in the polar coordinate system every point is represented in the plane with an ordered pair $\left( r,\theta \right)$ where $r$ is the distance from a reference point (conventionally origin) and $\theta $ is the angle from a reference direction (conventionally positive direction of $x-$axis) . The reference point is called the pole and the reference direction is called the polar axis. Here $r$ is called radial coordinate which is always positive and $\theta \in \left[ 0,2\pi \right)$ is called angular coordinate. \[\]
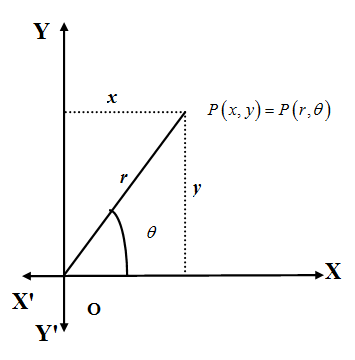
We can convert the Cartesian coordinate $\left( x,y \right)$ to polar coordinate $\left( r,\theta \right)$ of a point using the following relations
\[\begin{align}
& r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
& \theta =\operatorname{atan}2\left( y,x \right) \\
\end{align}\]
The function $\operatorname{atan}2\left( y,x \right)$ called 2-argument inverse tangent is defined as follows;
\[\theta =\left\{ \begin{matrix}
{{\tan }^{-1}}\left( \dfrac{y}{x} \right) & \text{if }x>0 \\
{{\tan }^{-1}}\left( \dfrac{y}{x} \right)+\pi & \text{if }x<0\text{ and }y\ge 0 \\
{{\tan }^{-1}}\left( \dfrac{y}{x} \right)-\pi & \text{if }x<0\text{ and }y<0 \\
\dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\
-\dfrac{\pi }{2} & \text{if }x=0\text{ and }y>0 \\
\text{undefined} & \text{if }x=0\text{ and }y=0 \\
\end{matrix} \right.\]
We are asked to convert $\left( -2,0 \right)=\left( x,y \right)$ which in Cartesian form to polar form. So we have the radial coordinate as
\[r=\sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{{{\left( -2 \right)}^{2}}+0}=\sqrt{4}=2\]
We see that in $\left( -2,0 \right)$ we have $x < 0,y\ge 0$.We find the angular coordinate is using the definition of 2-argument inverse tangent function as
\[\operatorname{atan}2\left( \left( -2,0 \right) \right)=\pi +{{\tan }^{-1}}\left( \dfrac{0}{-2} \right)=\pi +{{\tan }^{-1}}\left( 0 \right)=\pi +0=\pi \]
So the polar form of $\left( -2,0 \right)$ is $\left( 2,\pi \right)$ which is drawn below. \[\]

Note: We can convert back from polar coordinate $\left( r,\theta \right)$ to Cartesian coordinate $\left( x,y \right)$ using the conversion formula $x=r\cos \theta ,y=r\sin \theta $. We can alternatively find the polar angle $\theta $ as $\theta ={{\sin }^{-1}}\left( \dfrac{x}{r} \right)$. We note that the radial coordinate is always in radian. We also note that negative numbers are not used to represent polar coordinates unlike Cartesian coordinates.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




