
How do you convert $\dfrac{2\pi }{7}$ into degrees?
Answer
555k+ views
Hint: Here in this problem, we have to convert radians into degrees. One should know that 360 degrees = $2\pi $ radians. If you wish to convert any given angle from the measure of radians to degrees, the value has to be multiplied by $\dfrac{180}{\pi }$. Also, know that an angle which is subtended at the centre by an arc having a length equal to the radius of the circle.
Complete step-by-step solution:
Let’s solve the question now.
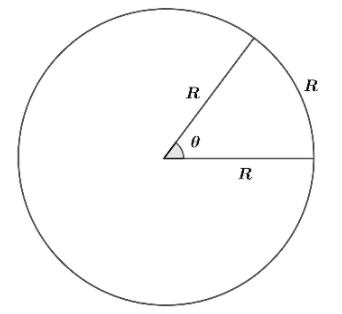
Let’s make a circle of ‘R’ radius and draw the arc of the same length ‘R’. So, when an angle $\theta $ is subtended at the centre by an arc length equal to the radius of the circle, then the angle is said to be one radian.
From the above figure, we can see that $\theta $ is the angle formed. If we want to find $\theta $, we divide arc length ‘S’ with the radius such that:
$\Rightarrow \theta =\dfrac{S}{R}$
As we know that one Revolution of a circle is equal to ${{360}^{\circ }}$ which is equal to $2\pi $ radians.
$\Rightarrow {{360}^{\circ }}=2\pi $radians
And now if ${{360}^{\circ }}=2\pi $ radians, then on dividing both sides by 2, we will get:
$\Rightarrow \dfrac{{{360}^{\circ }}}{2}=\dfrac{2\pi }{2}$
After reducing the terms, we get:
$\Rightarrow {{180}^{\circ }}=\pi $ Radians
If we wish to convert any radian to degree, we have to multiply the radian with a factor of $\dfrac{{{180}^{\circ }}}{\pi }$. So let’s convert $\dfrac{2\pi }{7}$ radians to degrees.
Multiply the given radian with $\dfrac{{{180}^{\circ }}}{\pi }$:
$\Rightarrow \dfrac{2\pi }{7}\times \dfrac{{{180}^{\circ }}}{\pi }$
Cancel $\pi $ :
$\Rightarrow \dfrac{2}{7}\times {{180}^{\circ }}$
Now multiply rest of the terms:
$\Rightarrow \dfrac{{{360}^{\circ }}}{7}\Leftrightarrow {{51.4}^{\circ }}$
So we got the angle in degrees.
Note: There is an alternative method too for this conversion. As we already know that degrees and radians can be written as i.e. ${{360}^{\circ }}=2\pi $radians. As the value of degrees will reduce, corresponding to it radians will also get reduced. So this is the scenario of direct proportion and can be solved by this method also. The radian is given i.e. $\dfrac{2\pi }{7}$ and the let degrees for this radian be ‘x’. So we can write it as:
$\Rightarrow \dfrac{{{360}^{\circ }}}{2\pi }=\dfrac{x}{\dfrac{2\pi }{7}}\Leftrightarrow \dfrac{{{360}^{\circ }}}{2\pi }=\dfrac{x\times 7}{2\pi }$
Now, keep ‘x’ alone and take all the terms on other side:
$\Rightarrow \dfrac{{{360}^{\circ }}\times 2\pi }{2\pi \times 7}=x$
Like terms will be cancelled:
$\Rightarrow \dfrac{{{360}^{\circ }}}{7}=x$
Solve for x:
$\therefore x={{51.4}^{\circ }}$
We got the same answer.
Complete step-by-step solution:
Let’s solve the question now.

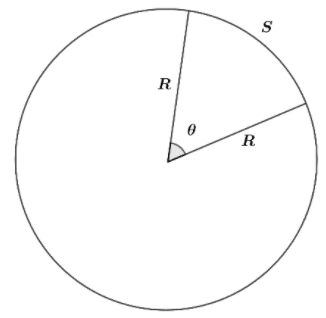
Let’s make a circle of ‘R’ radius and draw the arc of the same length ‘R’. So, when an angle $\theta $ is subtended at the centre by an arc length equal to the radius of the circle, then the angle is said to be one radian.
From the above figure, we can see that $\theta $ is the angle formed. If we want to find $\theta $, we divide arc length ‘S’ with the radius such that:
$\Rightarrow \theta =\dfrac{S}{R}$
As we know that one Revolution of a circle is equal to ${{360}^{\circ }}$ which is equal to $2\pi $ radians.
$\Rightarrow {{360}^{\circ }}=2\pi $radians
And now if ${{360}^{\circ }}=2\pi $ radians, then on dividing both sides by 2, we will get:

$\Rightarrow \dfrac{{{360}^{\circ }}}{2}=\dfrac{2\pi }{2}$
After reducing the terms, we get:
$\Rightarrow {{180}^{\circ }}=\pi $ Radians
If we wish to convert any radian to degree, we have to multiply the radian with a factor of $\dfrac{{{180}^{\circ }}}{\pi }$. So let’s convert $\dfrac{2\pi }{7}$ radians to degrees.
Multiply the given radian with $\dfrac{{{180}^{\circ }}}{\pi }$:
$\Rightarrow \dfrac{2\pi }{7}\times \dfrac{{{180}^{\circ }}}{\pi }$
Cancel $\pi $ :
$\Rightarrow \dfrac{2}{7}\times {{180}^{\circ }}$
Now multiply rest of the terms:
$\Rightarrow \dfrac{{{360}^{\circ }}}{7}\Leftrightarrow {{51.4}^{\circ }}$
So we got the angle in degrees.
Note: There is an alternative method too for this conversion. As we already know that degrees and radians can be written as i.e. ${{360}^{\circ }}=2\pi $radians. As the value of degrees will reduce, corresponding to it radians will also get reduced. So this is the scenario of direct proportion and can be solved by this method also. The radian is given i.e. $\dfrac{2\pi }{7}$ and the let degrees for this radian be ‘x’. So we can write it as:
$\Rightarrow \dfrac{{{360}^{\circ }}}{2\pi }=\dfrac{x}{\dfrac{2\pi }{7}}\Leftrightarrow \dfrac{{{360}^{\circ }}}{2\pi }=\dfrac{x\times 7}{2\pi }$
Now, keep ‘x’ alone and take all the terms on other side:
$\Rightarrow \dfrac{{{360}^{\circ }}\times 2\pi }{2\pi \times 7}=x$
Like terms will be cancelled:
$\Rightarrow \dfrac{{{360}^{\circ }}}{7}=x$
Solve for x:
$\therefore x={{51.4}^{\circ }}$
We got the same answer.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




