
How do you convert complex numbers from standard form to polar form and vice versa?
Answer
532.2k+ views
Hint: Assume any complex number of the standard form $z=x+iy$, where x is the real part and y is the imaginary part of z. Now, assume $\vec{r}$ as the radius vector of the point (x, y) and consider $\theta $ as the angle that this vector makes with the positive direction of x axis. Find the magnitude of the position vector by using the relation $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$ and write the polar form of the complex number given as: $z=r\left( \cos \theta +i\sin \theta \right)$.
Complete step by step answer:
Here, we have been asked to convert a complex number from its standard form to the polar form and from its polar form to the standard form. So, if we will get the relation between the two forms then we can easily convert it from one form to the other. Here, we will try to convert the standard form to the polar form.
Now, we know that the standard form of a complex number is $z=x+iy$, where x is the real part and y is the imaginary part of z. Here, the point (x, y) denotes the coordinates of the point which lies in the argand plane, a plane used to represent complex numbers. So, this point will have a position vector, denoted with $\vec{r}$ and it will subtend an angle $\theta $ with the positive direction of the x axis.
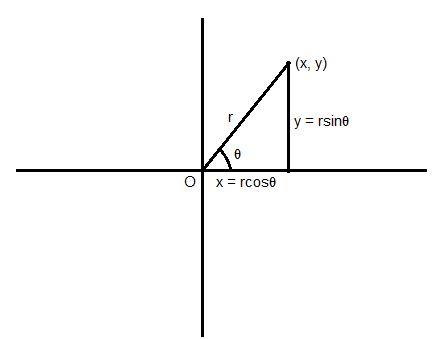
So, the magnitude of this position vector is given as $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$, because it forms a right angle triangle. The length of the base of this triangle will be $x=r\cos \theta $ and the length of the height will be $y=r\sin \theta $. Therefore, we can write the assumed complex number in polar form as:
$\begin{align}
& \Rightarrow z=r\cos \theta +ir\sin \theta \\
& \Rightarrow z=r\left( \cos \theta +i\sin \theta \right) \\
\end{align}$
Now, we have to calculate the value of $\theta $, so taking the ratio of y and x, we get,
$\begin{align}
& \Rightarrow \dfrac{y}{x}=\dfrac{r\sin \theta }{r\cos \theta } \\
& \Rightarrow \dfrac{y}{x}=\dfrac{\sin \theta }{\cos \theta } \\
& \Rightarrow \dfrac{y}{x}=\tan \theta \\
& \Rightarrow \tan \theta =\dfrac{y}{x} \\
& \Rightarrow \theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right) \\
\end{align}$
Therefore, the complex number in polar form becomes,
$\Rightarrow z=r\left( \cos \theta +i\sin \theta \right)$, where $\theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right)$ and $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$.
Hence, the above relation is our answer.
Note:
Now, if you are provided with the complex number in polar form $z=r\left( \cos \theta +i\sin \theta \right)$ and asked to convert it in the standard form then you can apply the reverse process of the steps that we have done above to get the relation. Here, the value of $\theta $ will depend on the quadrant in which the point (x, y) will lie. You may remember an important relation known as the Euler’s formula given as $\cos \theta +i\sin \theta ={{e}^{i\theta }}$, so the complex number can also be given as $z=r{{e}^{i\theta }}$.
Complete step by step answer:
Here, we have been asked to convert a complex number from its standard form to the polar form and from its polar form to the standard form. So, if we will get the relation between the two forms then we can easily convert it from one form to the other. Here, we will try to convert the standard form to the polar form.
Now, we know that the standard form of a complex number is $z=x+iy$, where x is the real part and y is the imaginary part of z. Here, the point (x, y) denotes the coordinates of the point which lies in the argand plane, a plane used to represent complex numbers. So, this point will have a position vector, denoted with $\vec{r}$ and it will subtend an angle $\theta $ with the positive direction of the x axis.

So, the magnitude of this position vector is given as $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$, because it forms a right angle triangle. The length of the base of this triangle will be $x=r\cos \theta $ and the length of the height will be $y=r\sin \theta $. Therefore, we can write the assumed complex number in polar form as:
$\begin{align}
& \Rightarrow z=r\cos \theta +ir\sin \theta \\
& \Rightarrow z=r\left( \cos \theta +i\sin \theta \right) \\
\end{align}$
Now, we have to calculate the value of $\theta $, so taking the ratio of y and x, we get,
$\begin{align}
& \Rightarrow \dfrac{y}{x}=\dfrac{r\sin \theta }{r\cos \theta } \\
& \Rightarrow \dfrac{y}{x}=\dfrac{\sin \theta }{\cos \theta } \\
& \Rightarrow \dfrac{y}{x}=\tan \theta \\
& \Rightarrow \tan \theta =\dfrac{y}{x} \\
& \Rightarrow \theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right) \\
\end{align}$
Therefore, the complex number in polar form becomes,
$\Rightarrow z=r\left( \cos \theta +i\sin \theta \right)$, where $\theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right)$ and $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$.
Hence, the above relation is our answer.
Note:
Now, if you are provided with the complex number in polar form $z=r\left( \cos \theta +i\sin \theta \right)$ and asked to convert it in the standard form then you can apply the reverse process of the steps that we have done above to get the relation. Here, the value of $\theta $ will depend on the quadrant in which the point (x, y) will lie. You may remember an important relation known as the Euler’s formula given as $\cos \theta +i\sin \theta ={{e}^{i\theta }}$, so the complex number can also be given as $z=r{{e}^{i\theta }}$.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




