Question

How do you convert 85 degrees 20’ into radians?

Answer 1

Hint: First of all convert 20’ into degrees by using the conversion relation: - \[1'=\dfrac{1}{60}\] degrees. Using this conversion, find the total angle, i.e., \[{{85}^{\circ }}20'\] in degrees. Now, understand the relation between the real number \[\pi \] and the angle corresponding to it in degrees. To do this, assume a circle of unit radius and use the relation: - \[\theta =\dfrac{l}{r}\] to establish the required relation between radian and degrees. Once the value of \[\pi \] radian is known in terms of degrees, find the value of 1 degree in terms of radian and use the unitary method to get the answer.

Complete step-by-step answer:
Here, we have been provided with the angle 85 degrees 20’ and we are asked to convert it into radian. But first we need to convert 20’ into degrees and determine the relation between radian and degrees.
Now, the angle \[{{85}^{\circ }}20'\] is read as 85 degrees 20 minutes. We know that \[60'={{1}^{\circ }}\], therefore we have,
\[\begin{align}
  & \Rightarrow 1'={{\left( \dfrac{1}{60} \right)}^{\circ }} \\
 & \Rightarrow 20'={{\left( \dfrac{20}{60} \right)}^{\circ }} \\
 & \Rightarrow 20'={{\left( \dfrac{1}{3} \right)}^{\circ }} \\
\end{align}\]
Therefore, we have the angle:
\[\begin{align}
  & \Rightarrow {{85}^{\circ }}20'={{85}^{\circ }}+{{\left( \dfrac{1}{3} \right)}^{\circ }} \\
 & \Rightarrow {{85}^{\circ }}20'={{85}^{\circ }}+{{\left( \dfrac{1}{3} \right)}^{\circ }} \\
 & \Rightarrow {{85}^{\circ }}20'={{\left( \dfrac{256}{3} \right)}^{\circ }} \\
\end{align}\]
Now, let us consider a circle with unit radius.

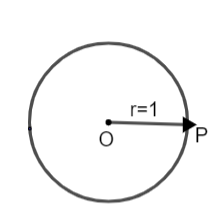
Consider a point P which starts moving on the circumference of this circle. We know that circumference of a circle is given as: - \[l=2\pi r\], here ‘l’ can be said as the length of the arc. Since, the radius is 1 unit, so we have,
\[\begin{align}
  & \Rightarrow l=2\pi \times 1 \\
 & \Rightarrow l=2\pi \\
\end{align}\]
Using the formula: - \[\theta =\dfrac{l}{r}\], we get,
\[\Rightarrow \theta =\dfrac{2\pi }{1}\]
\[\Rightarrow \theta =2\pi \] radian
Here, \[\theta \] represents the angle subtended by the initial and final position of the point P at the centre of the circle. Now, when this point P will return at the starting point then it will form an angle of \[2\pi \] radian but we know that it will form a complete angle, i.e., 360 degrees. So, we can relate the two units of measurement of angle as: -
\[\Rightarrow 2\pi \] radian = 360 degrees
\[\Rightarrow \pi \] radian = 180 degrees
Dividing both the sides with 180, we get,
\[\Rightarrow {{1}^{\circ }}=\left( \dfrac{\pi }{180} \right)\] radian
We have to find the value of \[{{\left( \dfrac{256}{3} \right)}^{\circ }}\] in terms of radian. So, multiplying both the sides with \[\dfrac{256}{3}\], we get,
\[\Rightarrow {{\left( \dfrac{256}{3} \right)}^{\circ }}=\left( \dfrac{256}{3}\times \dfrac{\pi }{180} \right)\] radian
On simplifying the R.H.S., we get,
\[\begin{align}
  & \Rightarrow {{\left( \dfrac{256}{3} \right)}^{\circ }}=\left( \dfrac{64}{3}\times \dfrac{\pi }{65} \right) \\
 & \Rightarrow {{\left( \dfrac{256}{3} \right)}^{\circ }}=\left( \dfrac{64\pi }{195} \right) \\
\end{align}\]
Hence, \[{{85}^{\circ }}20'\] measures \[\dfrac{64\pi }{195}\] radian.

Note: One may note that in trigonometry the term ‘minute’ and ‘second’ denotes the angle and not time so do not get confused. Always remember that: - \[60'={{1}^{\circ }}\] and \[60''=1'\] where 60’’ represents 60 seconds. Remember that ‘\[\pi \]’ is a real number and its value is nearly 3.14. Remember the result:\[\pi \] radian = 180 degrees. Note that these notations are used in higher trigonometry instead of degrees.