Question

How can converging lenses produce magnified images?
A. When object is in front of 2F
B. When object is at C
C. When object is at F
D. When object is behind the mirror

Answer 1

Hint: We can use lens formula to obtain an expression for distance of object from the optical centre. Then, this expression can be used along with a magnification formula in terms of object and image distance to obtain the position of the object for a magnified image. For an image to be magnified, its magnification must be greater than unity.

Complete step by step answer:
Focal length, image position and object position from the optical centre of a lens is related by Lens formula. According to lens formula,
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
Here, $f$, $v$ and $u$ are the focal length of the lens, distance of image from the optical centre and distance of object from the optical centre of lens respectively.
We rearrange this equation to obtain expression for distance of object from optical centre. That is,
$\dfrac{1}{u}=\dfrac{1}{v}-\dfrac{1}{f}=\dfrac{f-v}{vf}$
This implies that,
$u=\dfrac{vf}{f-v}$ ….. (1.1)
$\dfrac{v}{u}=\dfrac{f-v}{f}=1-\dfrac{v}{f}$ ….. (1.2)
Magnification of image is related to its position and object distance as
$m=\dfrac{v}{u}$
For an image to be magnified, the modulus of magnification must be greater than one. That is,
$\left| m \right|>1$
This implies that,
$\left| \dfrac{v}{u} \right|>1$
From equation (1.2)
$\left| 1-\dfrac{v}{f} \right|>1$
Modulus can be redefined as
$\left\{ \begin{align}
  & \begin{matrix}
   -1+\dfrac{v}{f} & if\,\dfrac{v}{f}>1 \\
\end{matrix} \\
 & \begin{matrix}
   1-\dfrac{v}{f} & if\,\dfrac{v}{f}<1 \\
\end{matrix} \\
\end{align} \right.$ ….. (2)
For $\dfrac{v}{f}>1$, we have
$-1+\dfrac{v}{f}>1$
This implies that,
$v > 2f$ ….. (3)
For $\dfrac{v}{f}<1$, we have
$1-\dfrac{v}{f}>1$
From this equation, no result can be derived. Therefore, we can conclude that the image is formed towards the right side of the lens.
From equation (3), it can be concluded that for a lens to produce a magnified image, the image must be positioned beyond $2f$. Let us find the position of the object from this.
$\dfrac{1}{u}=\dfrac{1}{v}-\dfrac{1}{f}$
We have, $v > 2f\Rightarrow \dfrac{1}{v}-\dfrac{1}{f}<\dfrac{1}{2f}-\dfrac{1}{f}\Rightarrow \dfrac{1}{u}<\dfrac{-1}{2f}$
This implies that,
$u > -2f$

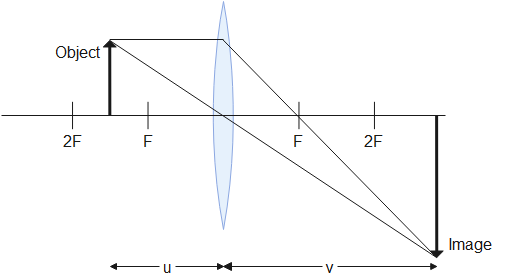
From this, we can conclude that converging lenses produce magnified images when the object is placed in front of 2F. Hence, option A is correct.

Note: Sign convention is must in optical lens and mirror problems. If sign convention is not proper the result is most likely to be wrong. The relation of position of image and position of image can be learned for solving these types of questions because this requires good command in mathematics and still is time consuming.