Question

Construct $\Delta \text{LMN}$in which $\text{LN = 7 cm}$, $\text{NM = 5}\text{.5 cm}$ and $\text{LM = 6}\text{.4 cm}$.

Answer 1

Hint: To construct a triangle with the lengths of three sides given, we will use a ruler and a compass. We will first draw a line segment of the given length using a ruler. Then we will fix the length of the second segment in the compass using the ruler. We will place the tip of the compass on one end point of the drawn segment and mark an arc using the compass for the second segment. Similarly, we will draw the third segment to construct the triangle.

Complete step by step answer:
Let us draw the first segment, which is $\text{LN = 7 cm}$. It will look like the following figure.

Now, we will fix the distance between the compass to be 5.5 cm, which is the length of the second segment. We will place the tip of the compass on the point N and mark an arc using the compass at a distance of 5.5 cm. Then, we will reset the distance in the compass to be equal to the length of the third segment, which is 6.4 cm. Now, we will place the tip of the compass at point L and mark an arc at a distance of 6.4 cm. The two arcs that we have just drawn should intersect at a point. This point of intersection is the vertex M of the triangle. It should look like the following figure,

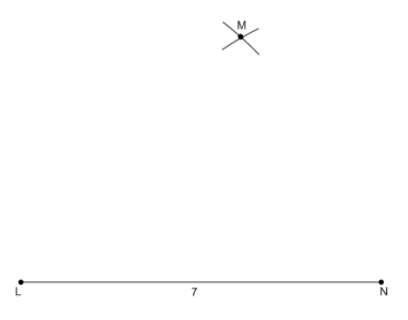
Next, we will join the points N and M to form segment NM. It will look like the following figure,

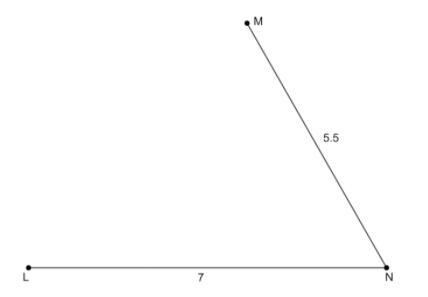
Then we will join the points L and M to form the third segment LM. We will get the required triangle of the specified side lengths and it will look like the following figure,

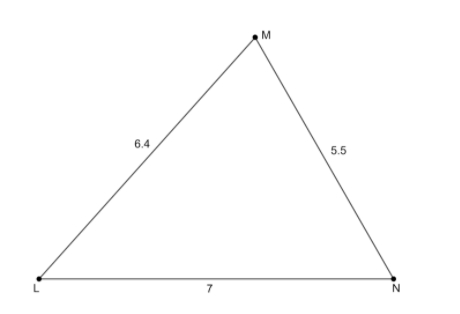
Note: The constructions in geometry should be very clear. It is beneficial to use a sharp pencil and a clean ruler and other instruments for construction. If there is a difference of even a millimeter in the given and actual measurements, then the construction will not be accurate and we might end up with a wrong figure. Hence, all geometric constructions require precision.