Question

Construct an isosceles triangle ABC in which base BC = 5.8 cm and altitude from A on BC is 4.8 cm.

Answer 1

Hint- Here, we will proceed by drawing the base of the required triangle and then, we will find the midpoint of the base and obtain the vertex A of the isosceles triangle ABC by drawing an arc having radius equal to the length of the altitude and centre as the midpoint of the base.

Complete step-by-step solution -
The steps of construction are given below:
Step1: Draw a line segment of length 5.8 cm using a scale. Name the endpoints of this line segment as B and C. This BC represents the base of the isosceles triangle ABC.

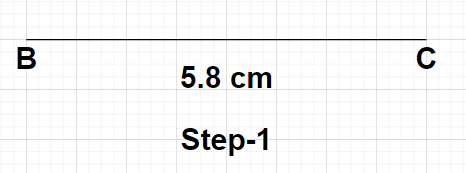
Step2: Draw a perpendicular bisector of this line segment BC using compass. Mark the point where this perpendicular bisector is drawn cuts the line segment BC as point P. Here, point P is the midpoint of the line segment BC because the perpendicular bisector of any line, divides that line equally and at ${90^0}$.

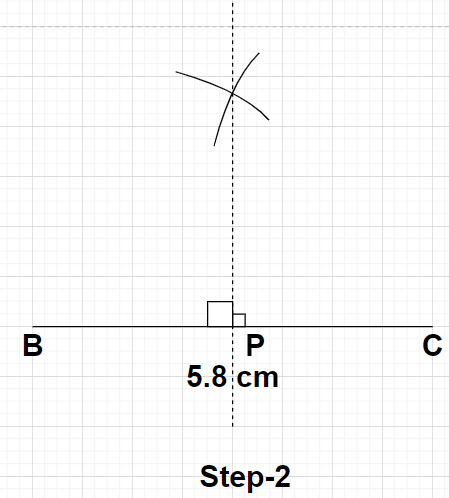
Step3: Now, taking point P as the centre draws an arc having a radius of 4.8 cm (which is measured using the scale) with the help of a compass. Name the point where this arc cuts the perpendicular bisector as point A. Now, join point A with points B and C respectively. These lines AB and AC represent the other two sides of the isosceles triangle ABC.
Here, if we will measure the length of the sides AB and AC with the help of a scale. They will give equal measures and in any isosceles triangle, the length of two sides are equal in measure.

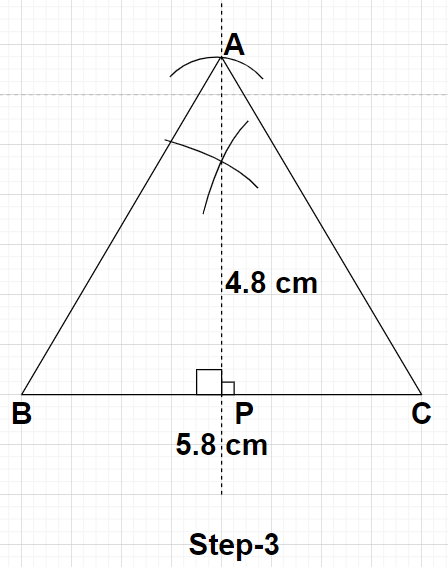
So, we will be having AB and AC as the equal sides of the isosceles triangle.

Note- In this particular problem, the perpendicular bisector of the line segment BC is drawn by opening the compass more than half the length of the line segment BC (i.e., more than 2.9 cm). Then, placing the fixed end of the compass at point B and drawing an arc. Similarly, placing the fixed end of the compass at point C and cutting the already drawn arc and then drawing a perpendicular from this meeting point to the line segment BC.