Question

Construct an equilateral triangle, given its side and justify the construction.

Answer 1

Hint: We know that in an equilateral triangle all sides are equal. First draw the one side of the triangle which will be given in the question. We will use this line end point as two vertices of the triangle. Now our task is to find a third point which has equal distance from both ends. Now draw two arcs from both ends which radii are equal to the length of line. The intersection point of both arcs is our third point. This will have equal distance from both ends. Finally join this point to both ends and we will have the required triangle.

Complete step-by-step answer:
Let’s assume that the side of the equilateral triangle is given ‘a’ cm.
We will be going through the following steps to draw an equilateral triangle of ‘a’ cm.
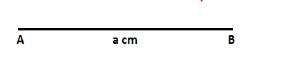
Draw a line segment AB of length ‘a’ cm.
 

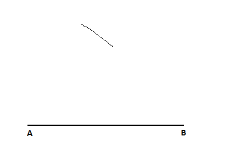
Taking ‘a’ cm as radius, and A as centre, draw an arc.
 

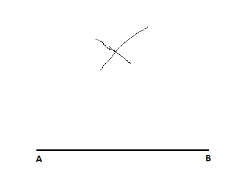
Taking ‘a’ cm as radius, and B as centre, draw another arc.
 

Let C be the point where the two arcs intersect . Join AC and BC and label the sides.
 

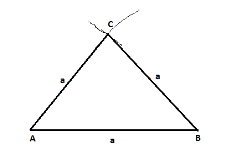
Thus, ABC is the required equilateral triangle.

Justification;
By construction, AB = AC = BC (Radius of equal arcs)
Since, all sides are equal, therefore, ABC is an equilateral triangle.

Note: And altitude of the equilateral triangle bisects its base and opposite angle. By using this information we can also construct an equilateral triangle.