Question

Construct an angle of measure ${{22.5}^{\circ }}$ using compass and ruler.

Answer 1

Hint: We must first draw an angle of ${{90}^{\circ }}$, which we will need to bisect so that we have an angle of measure ${{45}^{\circ }}$. We know that ${{22.5}^{\circ }}$ is the half of ${{45}^{\circ }}$, so we can find the required angle by bisecting the ${{45}^{\circ }}$ angle.

Complete step by step answer:
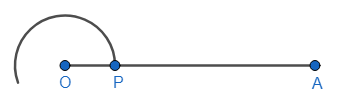
Let us first construct a straight-line OA as the base line, with reference to which, we will draw an angle of ${{22.5}^{\circ }}$.

Now, we must take a suitable radius in the compass, and draw an arc with O as centre and intersecting the line OA at point P. So, our figure must now look something like the one shown below.

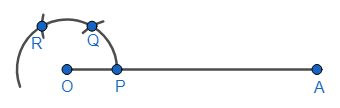
For the next step, we must draw an arc, with the same radius and P as centre, that cuts this previous arc at point Q. We know that this new arc represents an angle of ${{60}^{\circ }}$.
Now, with Q as centre and the same radius, we must draw another arc intersecting the big arc at R. We know that this point R represents an angle of ${{120}^{\circ }}$.
So, now our figure must look something like the one shown below.

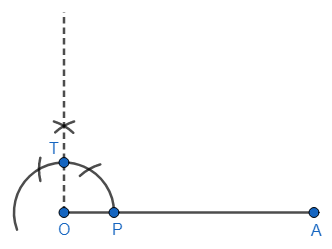
We first need to draw an angle of ${{90}^{\circ }}$. So, now with Q as centre and a suitable radius, we must draw an arc in the upper part of the distance between Q and R. And, then with the same radius, but R as centre, we must draw an arc intersecting the previous arc at point S. We now join OS to get an angle of ${{90}^{\circ }}$. Let us assume the intersection of this ${{90}^{\circ }}$ line with the first big arc be T.

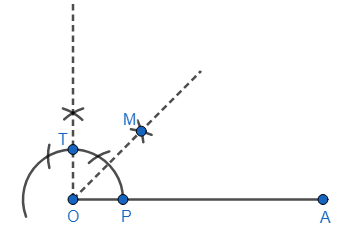
Now, we need to bisect this right angle to get an angle of ${{45}^{\circ }}$.
So, with a suitable radius and P as centre, we will draw an arc in the interior of this right angle. And then, with the same radius, but T as centre, we will draw another arc intersecting this previous arc at M. We can now join OM, which we know represents an angle of ${{45}^{\circ }}$.

Let the intersection of OM with the first big arc be at point N. Again, we need to bisect the angle. So, we will take P as the centre and a suitable radius and draw an arc. Then, with N as centre and same radius, we will draw an arc intersecting the previous arc at B. We can now join OB.

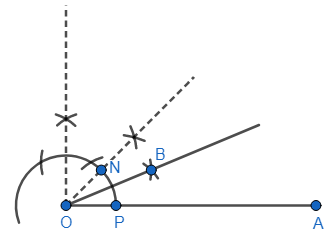
The required angle is $\angle AOB$ and its measure is ${{22.5}^{\circ }}$.

Note: We can also solve this problem by first bisecting ${{60}^{\circ }}$into ${{30}^{\circ }}$ and again bisecting this ${{30}^{\circ }}$ to get ${{15}^{\circ }}$. Also, we must note here that ${{22.5}^{\circ }}={{15}^{\circ }}+{{7.5}^{\circ }}$, where ${{7.5}^{\circ }}$ can be found by bisecting the ${{15}^{\circ }}$ angle.