Question

Construct AB = 8.5cm. Divide it in the ratio 5:7. Write steps of construction

Answer 1

Hint: Use basic proportionality theorem to divide the line segment in the ratio 5:7. Create a line segment in which we know the point which divides that line segment in 5:7 ratio with an acute angle to the given line segment. Form a triangle with these line segments. Through the 5:7 division point of the created line segment, draw a line parallel to the base of the triangle. The point at which this line intersects the original line segment will be the 5:7 division point,

Complete step-by-step answer:

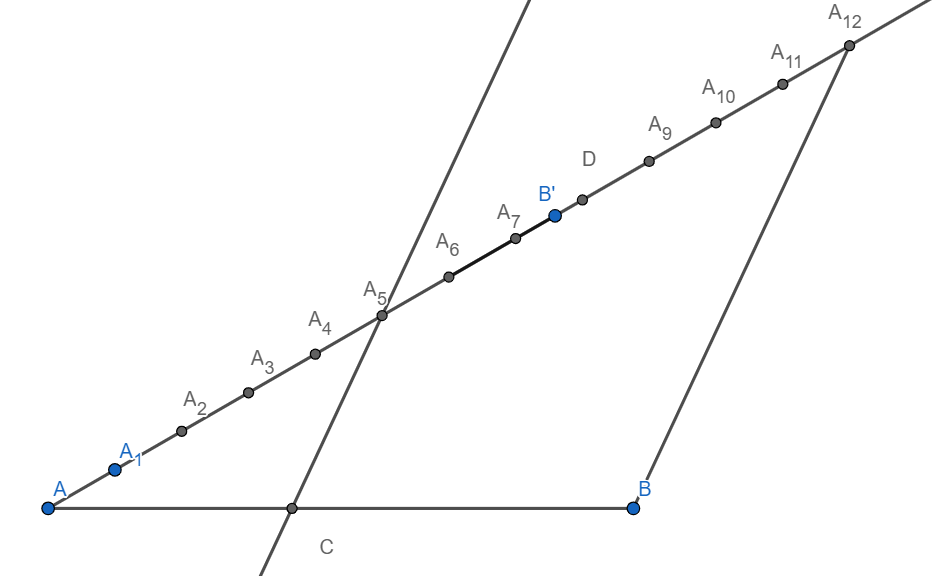
Steps of construction:
[1] Draw a line segment AB = 8.5 cm.
[2] Construct an acute angle B’AB.
[3] Mark 12 equidistant points on B’A such that $A{{A}_{1}}={{A}_{1}}{{A}_{2}}=\cdots ={{A}_{11}}{{A}_{12}}$
[4] Join ${{A}_{12}}B$
[5] Through ${{A}_{5}}$ draw a line parallel to ${{A}_{12}}B$
[6] Let the line intersect AB at C.
[7] Hence C is the point which divides AB in the ratio 5:7.

Note: Justification of the construction:
Since ${{A}_{5}}C\parallel {{A}_{7}}B$ we have by basic proportionality theorem
$\dfrac{A{{A}_{5}}}{A{{A}_{12}}}=\dfrac{AC}{AB}$
We know that $A{{A}_{5}}=5A{{A}_{1}}$ and $A{{A}_{12}}=12A{{A}_{1}}$
Hence $\dfrac{AC}{AB}=\dfrac{5}{12}$
We know that $\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow \dfrac{a}{b-a}=\dfrac{c}{d-c}$
Using, we get
$\dfrac{AC}{AB-AC}=\dfrac{5}{12-5}$
But AB-AC = BC
Hence, we have
$\dfrac{AC}{BC}=\dfrac{5}{7}$
Hence C divides AB in the ratio of 5:7.