Question

Construct a triangle whose sides are 4 cm, 6 cm and 8 cm. Draw the circumcircle of the triangle.

Answer 1

Hint: Let the triangle be $\Delta $ PQR. Take QR = 8 cm side as the base. Take Q as centre and draw an arc of 4 cm. Similarly, take R as centre and draw an arc of 6 cm intersecting the previous arc. Join the intersection of these arcs to Q and R. This is the triangle. Now draw perpendicular bisectors of all the sides intersecting at O. With O as centre and OP as radius, construct a circle which will pass through Q and R. This is the circumcircle.

Complete step-by-step answer:

We need to construct a triangle whose sides are 4 cm, 6 cm and 8 cm and then draw the circumcircle of the triangle.
Follow the given steps to solve the question.
First, we will construct the triangle. Let us name the triangle as $\Delta $ PQR.
Following are the steps to construct $\Delta $ PQR:
1. Let the base of the triangle be QR = 8 cm.
2. Taking Q as the centre and radius 4 cm on the compass, draw an arc on the upper side of QR.
3. Taking R as the centre and radius 6cm on the compass, draw an arc on the upper side of QR, intersecting the previous arc. Mark this point of intersection as point P.
4. Join points P to Q and P to R to complete the $\Delta $ PQR.
Now, we need to draw the circumcircle of the triangle. For this, we will first draw the perpendicular bisectors of all the sides of the triangle in the following steps:

1. Taking Q as the centre and radius more than half of QR, mark arcs below and above the line.
2. Now, with R as the centre and same radius, draw arcs above and below the line to intersect the already drawn arcs. Name the new points as X and Y.
3. Join points X and Y. This line XY is the required perpendicular bisector of side QR.
4. Similarly, draw perpendicular bisectors of sides PQ and PR.

Now, we will construct the circumcircle of $\Delta $ PQR. To do so, follow the given steps:
1. All the perpendicular bisectors of $\Delta $ PQR will intersect at one point. Name that point as O.
2. Taking point O as the centre and OP as the radius draw a circle. Points Q and R should also lie on this circle.
3. This is the required circumcircle.

The final figure will look like this:

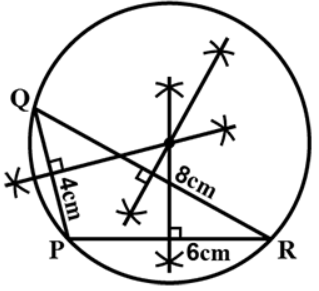
Note: First check whether it is possible to construct the given triangle using triangle inequality property. The triangle inequality property states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side. We see that our triangle satisfies this and hence, it is possible to construct such a triangle.