Question

Construct a triangle \[PQR\] in which $QR = 6cm$, $\angle Q = 60^\circ $ and $PR - PQ = 2cm$

Answer 1

Hint: Here, we need to construct a triangle $PQR$. Let us consider $QR = 6cm$as the baseline of the required triangle. And then using $\angle Q = 60^\circ $, we need to draw a ray. We shall extend the line below the baseline and using $PR - PQ = 2cm$as a radius, we need to draw an arc and join It with $R$. Then we shall draw perpendicular bisectors and join all the required points.

Complete answer:
Here we are given $QR = 6cm$, $\angle Q = 60^\circ $ and $PR - PQ = 2cm$and we need to construct a triangle.
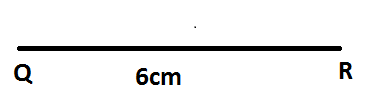
Step $1$: We are given $QR = 6cm$and we shall consider $QR = 6cm$as the base of the required triangle.
So we need to draw a line using a ruler measuring $QR = 6cm$.

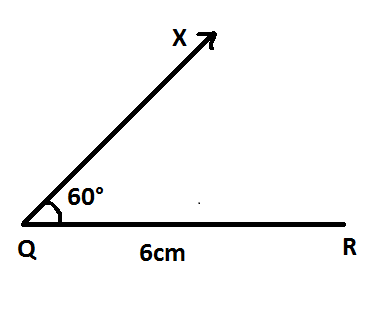
Step $2$: Also, we are given $\angle Q = 60^\circ $. Now, we need to make an angle of $60^\circ $ at $RQX$ using a protractor.

Step $3$: Now, we need to extend the line below $QR$. Next, we shall consider $Q$ as center and radius as $2cm$and we need to draw an arc to intersect the ray $QY$ at $Z$where $QZ = PR - PQ = 2cm$
Here, $PR - PQ = 2cm$$ \Rightarrow PR > PQ$
Also, $PQ - PR$ is negative and so $QZ = PR - PQ = 2cm$will be below the baseline $QR$

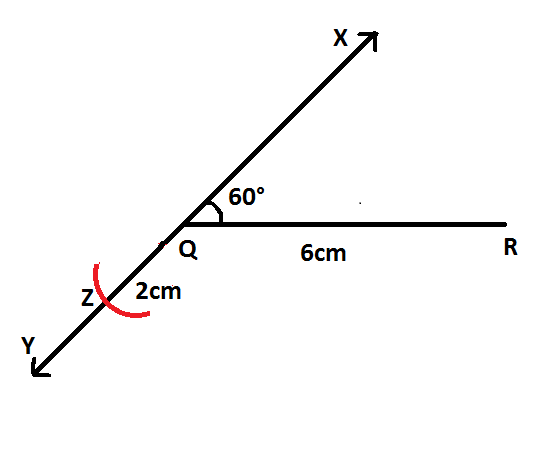
Step $4$: Now, we shall join $RZ$.

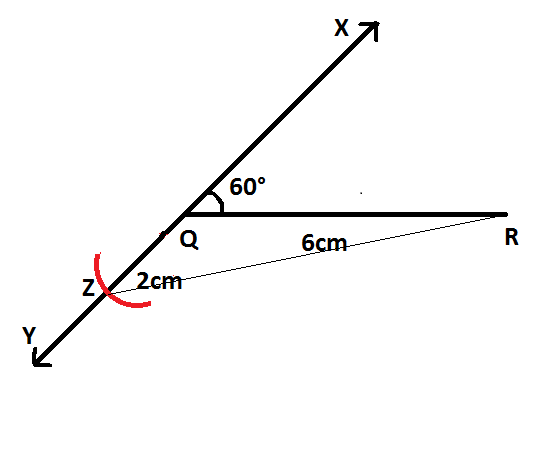
Step $5$: We need to construct a perpendicular bisector of $ZR$. To draw the required perpendicular bisector, with $Z$ and $R$ as center separately and radius greater than half of $ZR$, we shall draw arcs on either side to intersect each other.
Also, we shall join the intersecting points and extend them to meet the ray $QX$ at $P$ .

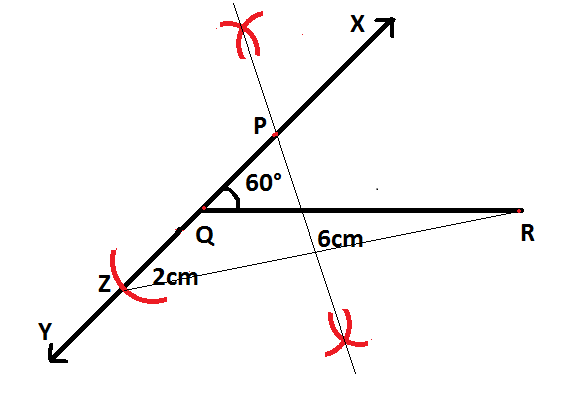
Step $6$: At last we need to join $P$ and $R$. Now, we will obtain the required triangle $PQR$
The required constructed triangle $PQR$is as follows.

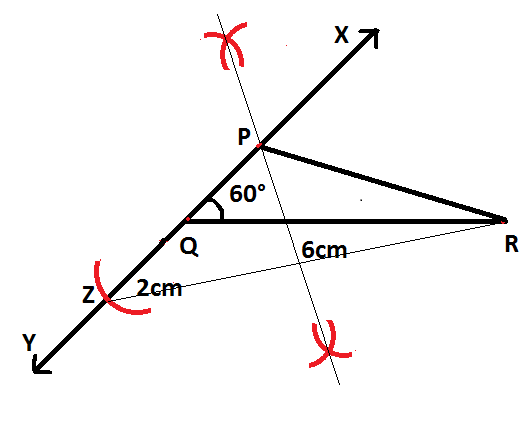
Note: To draw a perpendicular bisector, we need a line segment $ZR$. Then, with a radius a little more than half of the length of $ZR$and \[Z\] as the center, we need to draw arcs above and below the line $ZR$. Again, with a radius a little more than half of the length of $ZR$and $R$ as the center, we need to draw arcs above and below the line $ZR$. Then, using a ruler just draw a line connecting both arcs and we will get the required perpendicular bisector.