Question

Construct a triangle of side \[4{\text{ cm}}\] , \[{\text{5 cm}}\] and \[{\text{6 cm}}\] and then a triangle similar to it whose sides are \[\dfrac{2}{3}\] of the corresponding sides of the first triangle. Give the justification of the construction.

Answer 1

Hint: We are going to use the concepts of similarity and construct the diagram. Also, we will learn about the way to construct a triangle, and some rules that have to be followed before constructing a triangle. We will also know a little about the similarity of triangles.

Complete step by step solution:
Generally, in a triangle, the sum of lengths of any two sides is always greater than the third side.
Suppose, if sides of a triangle are of lengths \[a,b{\text{ and }}c\] , then \[a + b > c\] , \[a + c > b\] and \[b + c > a\] .
So, if these conditions are not satisfied, then we cannot construct a triangle.
So, now let’s check the conditions for given sides.
Here, the sides are of length \[4{\text{ cm}}\] , \[{\text{5 cm}}\] and \[{\text{6 cm}}\] .
So, \[4 + 5 > 6\] and \[5 + 6 > 4\] and \[4 + 6 > 5\]
So, all the conditions are satisfied, so a triangle can be constructed.
To construct a triangle, follow these steps:
(1) Draw a line segment \[AB = 6{\text{ cm}}\]

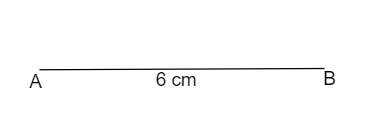
(2) With “B” as centre, draw an arc of radius \[5{\text{ cm}}\] .

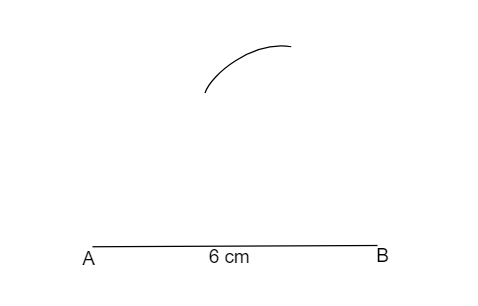
(3) Now, with “A” as centre, draw an arc of radius \[4{\text{ cm}}\] , which cuts the previous arc at “C”.

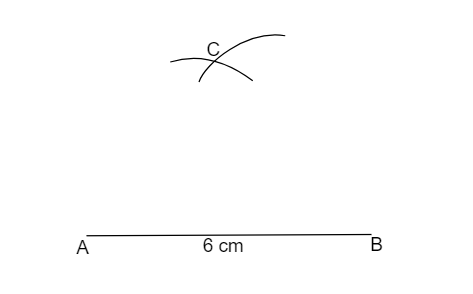
(4) Join A and C, to get \[AC\] and join B and C, to get \[BC\]

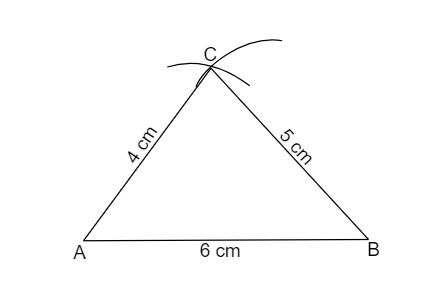
(5) This is the required first triangle.
Now, we need to construct another triangle whose sides are \[\dfrac{2}{3}\] of the corresponding sides of the first triangle.
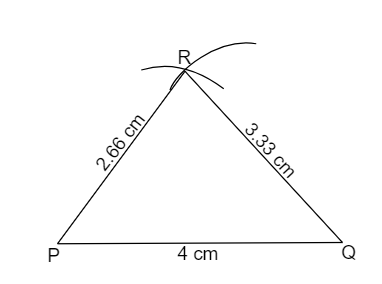
Let the triangle be \[\vartriangle PQR\] where, \[PQ = \dfrac{2}{3}AB\] and \[QR = \dfrac{2}{3}BC\] and \[RP = \dfrac{2}{3}CA\]
\[ \Rightarrow PQ = \dfrac{2}{3}(6) = 4{\text{ cm}}\] and \[QR = \dfrac{{10}}{3}{\text{ cm}}\] and \[RP = \dfrac{8}{3}{\text{ cm}}\]
So, now construct \[\vartriangle PQR\] in the same way, in which we constructed the first triangle.
Draw a line segment \[PQ = 4{\text{ cm}}\] . Then with “Q” as centre, draw an arc of radius \[\dfrac{{10}}{3}{\text{ cm}}\] , then with “P” as centre, draw an arc of radius \[\dfrac{8}{3}{\text{ cm}}\] which cuts the previous arc and you will get the point “R”. Join \[PR\] and \[QR\] . And this is the required triangle similar to the first triangle.

Note: Two triangles are said to be similar, if their corresponding sides are in the same ratio. And also, in similar triangles, the corresponding angles are equal. If the ratios are \[1:1\] , then the corresponding sides are equal and the two triangles are said to be congruent. All congruent triangles are similar, but all similar triangles may or may not be congruent.