Question

Construct a triangle ABC such that \[\angle B = {60^ \circ },\angle C = {45^ \circ }\] and AB + BC + CA = 10 cm.

Answer 1

Hint: We will first construct a straight line of 10 cm and then do the required next construction and write all of the steps of construction and draw it as well. Thus, we will get the answer.

Complete step-by-step solution:
We will first write the steps of construction and then finally draw the required figure.
Steps of Construction:-
Step 1: First of all, draw a line XY with length 10 cm since we are given that AB + BC + CA = 10 cm.

Step 2: Since we are given that \[\angle B = {60^ \circ }\] and \[\angle C = {45^ \circ }\], therefore, we will now draw the angles $\angle LXY = {60^ \circ }$ and $\angle MYX = {45^ \circ }$.

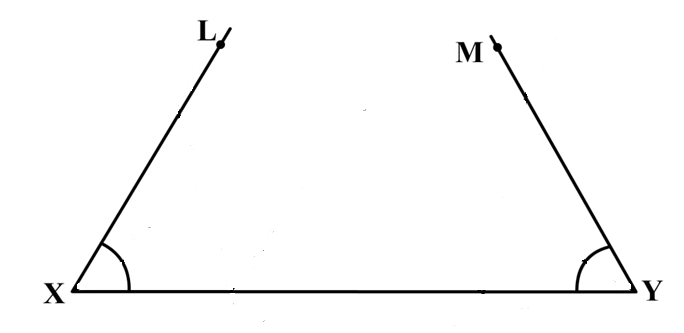
Step 3: Now we will just bisect angle $\angle LXY = {60^ \circ }$ and $\angle MYX = {45^ \circ }$ using a compass. Just place the compass on the circular part of the angle on both sides and make an arc. Join the intersection of arcs.

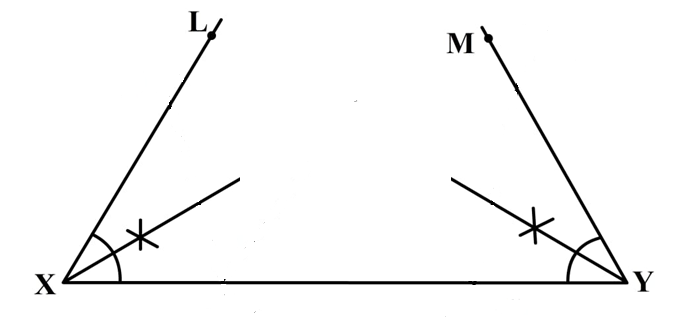
Step 4: Join both the lines that are where the bisectors meet and name the point as A.

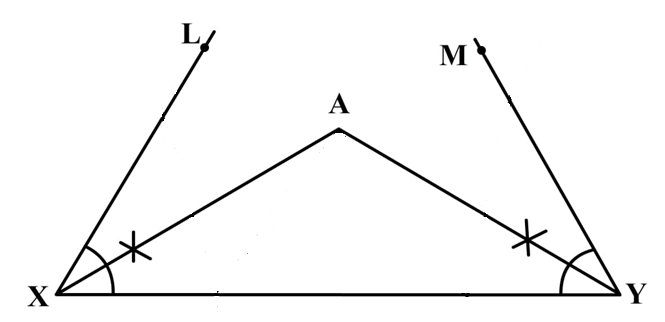
Step 5: Now, we will draw perpendicular bisectors PO and RS of AX and AY respectively by drawing arcs from both sides of each line opening the compass more than half of the length of line.

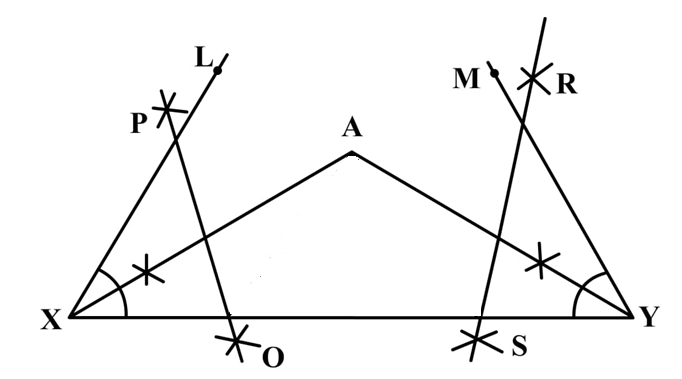
Step 6: Now, wherever PO cuts XY, name that point as B and wherever RS cuts XY, name it as C.

Step 7: We will now join AB and AC.

Thus, we have the required triangle ABC and shown above.

Note: The students might be worried about whether they got the required triangle or not. They may check it using a protractor for their own satisfaction and then verify the lines length by ruler.
The students must keep in mind that their protractor needs to be tight enough so that whenever they are drawing, it is not going all over the place in order to get the triangle with required properties.