Question

Construct a triangle ABC in which \[BC = 7\,\,cm\], \[\left| \!{\underline {\,
  B \,}} \right. = {75^ \circ }\] and \[AB + AC = 13\,cm\].

Answer 1

Hint:Here in this question belongs to the construction topic. To construct a triangle, given its base, a base angle and sum of other two sides we have to construct step-by-step by using a geometrical- instruments like centi-meter scale, compass with provision of fitting a pencil and protractor.

Complete step by step answer:
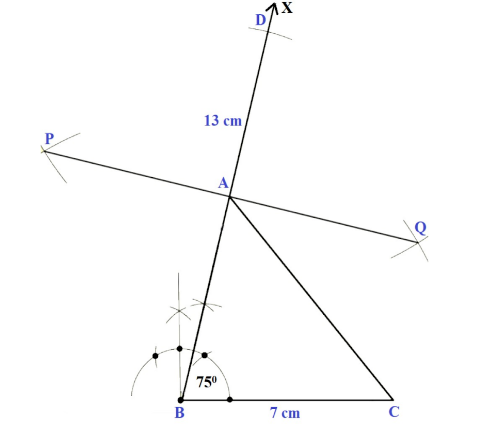
Consider the given question: given the base \[BC = 7\,\,cm\], a base angle, \[\left| \!{\underline {\,B \,}} \right. = {75^ \circ }\] and the sum \[AB + AC = 13\,cm\] of the other two sides to construct a triangle $ABC$. To construct the triangle $ABC$, follow the below steps:

Steps of Construction:
-Draw the baseline $BC$ of length 7 cm i.e., \[BC = 7\,\,cm\].
-At the point \[B\] make an angle \[\left| \!{\underline {\,B \,}} \right. = {75^ \circ }\] and produce it upto \[BX\], say \[\left| \!{\underline {\,{XBC} \,}} \right. \] equal to the given angle.
-Cut a line segment with $B$ as centre and draw an arc \[BD = 13\,cm\] equal to \[AB + AC\] from the ray $BX$.
-Now, draw a perpendicular bisector $PQ$ of line $BD$. i.e., Take ‘$B$’ as centre and radius more than half of the length of line $BD$, draw an arc in both left and right direction of line $BD$ and do the same by taking ‘$D$’ as centre with the same radius. Then join the arc intersection point $P$ and $Q$.
-Make a name ‘$A$’ which the point of the perpendicular bisector $PQ$ intersects the line $BD$.
-Join the Point $AC$.

Then the required triangle \[\vartriangle ABC\] is:

Note: When doing construction handling the instruments carefully, when making an angle the radius or arc will be the same which cannot be altered. If we can verify the construction easily by measuring the length of side $AB$ and $AC$ in above construction using a centi-meter scale their sum should be equal to the length of $BD$ i.e., \[AB + AC = BD\]. Remember the construction of the triangle is not possible if the sum \[AB + AC \leqslant BD\].