Question

Construct a right angle triangle whose hypotenuse is 6 cm long and one of the legs is 4 cm long.

Answer 1

Hint: Use Pythagoras theorem to determine the third side of the triangle. Now, draw the 4 cm leg and then from its one end draw a perpendicular line and extend it. From the other end of the 4 cm leg cut a length of 6 cm on the extended line.

Complete step-by-step answer:

We know that the sum of two sides of a triangle is greater than the third side and the difference of two sides is smaller than the third side. Now, construction in geometry means to draw shapes, angles or lines accurately. These constructions use only compass, ruler or straightedge and a pencil. This is the pure form of geometric construction and no numbers are involved. Sometimes, protractors can be used to draw angles that cannot be drawn with the help of compass. Now, compasses are drawing instruments used for drawing circles and arcs. A ruler is used to draw a straight line. Construction is a very useful topic in maths. By the help of construction can easily prove whether a geometrical shape can be drawn or not.
Now, let us come to the question:
One side of the given right angled triangle is 4 cm and hypotenuse is 6 cm.
Therefore, using Pythagoras theorem: ($hypotenus{{e}^{2}}=bas{{e}^{2}}+perpendicula{{r}^{2}}$), we get, third side of the right angle triangle $=\sqrt{{{6}^{2}}-{{4}^{2}}}=\sqrt{20}$ cm.
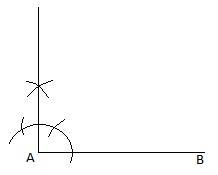
Now, draw a side of 4 cm. Name the line segment AB. Draw a line perpendicular to AB by putting a protector on A. Now, extend this line. Then, put the compass on B and cut an arc of length 6 cm on the extended line.

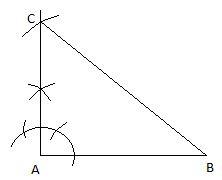
Hence, our construction is complete.

Note: One may get confused as to why we have drawn 4 cm side initially and not the other side. This is because we cannot draw $\sqrt{20}$ cm with our ruler. Also, keep the pencil sharp and use a soft hand to draw. Measurement should be accurate.