Question

Construct a Rhombus \[ABCD\], given its diagonal $AC = 6.3$ cm and diagonal $BD = 5.5$ cm

Answer 1

Hint: The general idea is to first draw a straight line $AC = 6.3$cm with a compass, which will be our reference line. We will use the fact that the two diagonals of a Rhombus intersect each other at right angles also they bisect each other. Then by using a compass and ruler we will draw a perpendicular bisector of line segment \[AC\].
We can measure half of the distance of $5.5$ and mark it and then the required rhombus can be drawn.

Complete step-by-step answer:
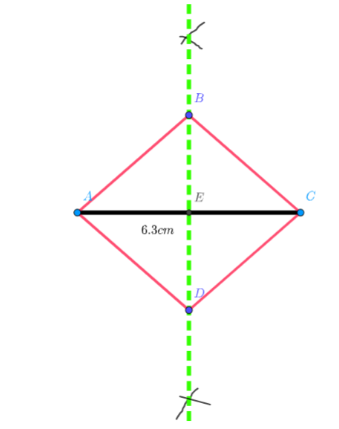
Draw a line segment \[AC\] of length $6.3$ cm which will be our line of reference.

Using a compass we will draw a perpendicular bisector of \[AC\]:
First use the compass for marking the arc intersection drawn from points \[A\] and \[B\].

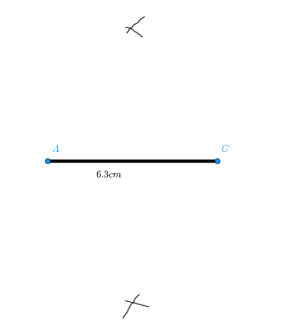
Now draw the perpendicular bisector of the line segment\[AC\].

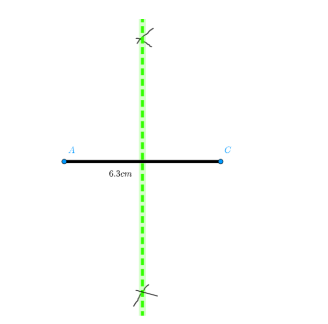
Mark the point of intersection of the perpendicular bisector as $E$.

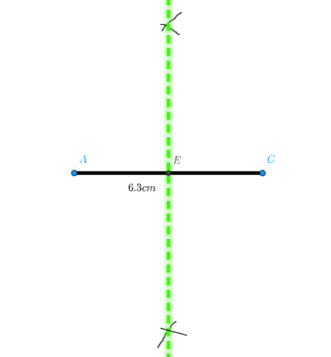
Using a ruler we will mark points $B$ and $D$ which are from a distance of $\dfrac{{5.5}}{2} = 2.75$cm from $E$ along the green dotted line (perpendicular bisector of the line segment \[AC\]) .
The above fact is used because $BD$ is a diagonal of the rhombus and the diagonals of a rhombus bisect each other.

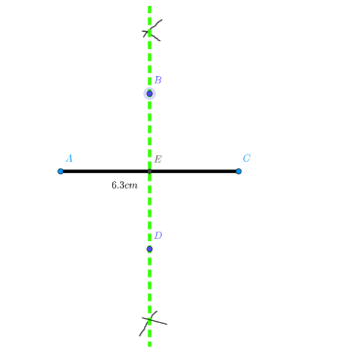
Now after this construction we can join the marked points.
Now join the lines $AB,AD,DC,CB$.

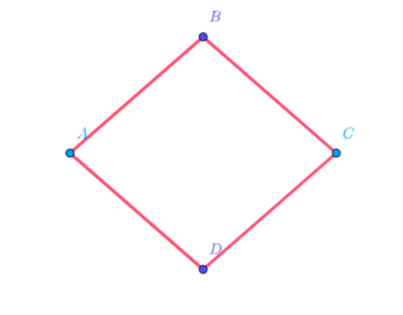
This is the required rhombus.

Note: Make the proper use of ruler and compass. A very small measurement may not hamper the whole construction but it may make the solution look ugly. We have used the line segment \[AC\] to draw the rhombus while the same can be drawn using $BD$ with the same process.