Question

Construct a quadrilateral ABCD in which \[AB=4cm\], \[AC=5cm\], \[AD=5.5cm\] and \[\angle ABC=\angle ACD={{90}^{\circ }}\]

Answer 1

Hint: We solve this problem by constructing the quadrilateral using steps from angle to side length. First, we take a reference axes then we construct angle \[\angle ABC\] which is easy by using the protractor then we use the compass or ruler to construct the sides of the quadrilateral which gives the required quadrilateral.

Complete step-by-step solution
We are given that for a quadrilateral ABCD such that \[AB=4cm\], \[AC=5cm\], \[AD=5.5cm\] and \[\angle ABC=\angle ACD={{90}^{\circ }}\]
Let us construct the angle \[\angle ABC={{90}^{\circ }}\] of some unknown length as

Now let us point the vertex A on the ray BY such that \[AB=4cm\] then we get

Now, let us point the vertex C on the ray BX such that \[AC=5cm\] then we get

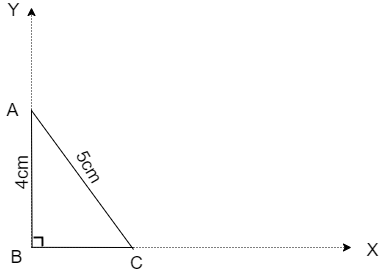
We are given with another angle that is \[\angle ACD={{90}^{\circ }}\]
Now, let us construct a ray CZ such that \[\angle ACD={{90}^{\circ }}\] using the protractor then we get

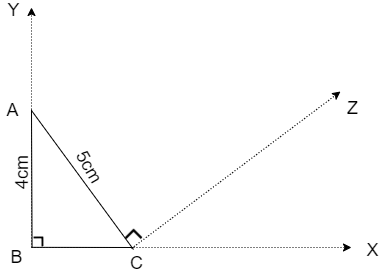
Now, let us point the vertex D on the ray CZ such that \[AD=5.5cm\] then we get

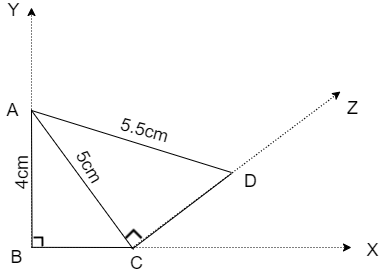
Now by removing the rays and drawing the quadrilateral ABCD we get

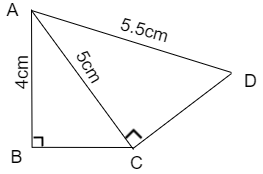
Therefore, we can say that the quadrilateral ABCD such that \[AB=4cm\], \[AC=5cm\], \[AD=5.5cm\] and \[\angle ABC=\angle ACD={{90}^{\circ }}\] has been constructed.

Note: The question can be extended furthermore that is to find the length of BC and CD.
We use the Pythagoras theorem for finding the length of BC and CD
We know that the Pythagoras Theorem states that the square of the hypotenuse is equal to the sum of squares of the other two sides that is for the triangle shown below