Question

Construct a parallelogram ABCD, when diagonal AC=6.4 cm, diagonal BD=8.2 cm and the angle between the diagonal is equal to ${60^0}$. What is the value of the perimeter of the parallelogram ABCD (in cm)? (Round off your answer to the nearest integer)

Answer 1

Hint: Here, we will proceed by drawing the diagonals AC of length 6.4 cm and BD of length 8.2 cm with the help of scale, compass and protractor. Then, we will join the points A, B, C and D in order to get the parallelogram ABCD.

Complete step-by-step answer:
The various steps of construction required to draw parallelogram ABCD are mentioned below:
Step1- Draw a line segment of length 6.4 cm with the help of a scale. Name the end points of this line segment as A and C respectively. This line segment AC is the diagonal of the parallelogram. Now, using compass bisect the line segment AC in order to get the midpoint of this line segment AC. Mark this midpoint of line segment AC as point M where AM=MC=$\dfrac{{{\text{AC}}}}{2} = \dfrac{{{\text{6}}{\text{.4}}}}{2} = 3.2$ cm.

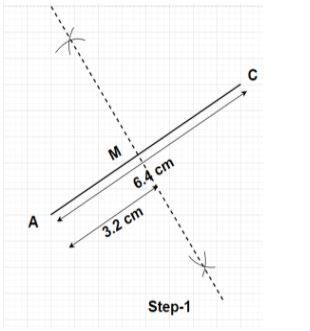
Step2- Since, the angle between the diagonals AC and BD of the parallelogram ABCD is equal to ${60^0}$. Using the protractor, from point M draw a dotted line segment inclined at ${60^0}$ with the diagonal AC. According to the property of the parallelogram, the diagonals of the parallelogram bisect each other (i.e., the diagonals of the parallelogram intersect at the midpoint). So, midpoint M of the diagonal AC is also the midpoint of the diagonal BD. Hence, BM=MD=$\dfrac{{{\text{BD}}}}{2} = \dfrac{{{\text{8}}{\text{.2}}}}{2} = 4.1$ cm. Now make two arcs on the dotted line segment which is inclined to the diagonal AC at ${60^0}$ from point M on the both sides each of length 4.1 cm. Name these points as B and D as shown in the figure.

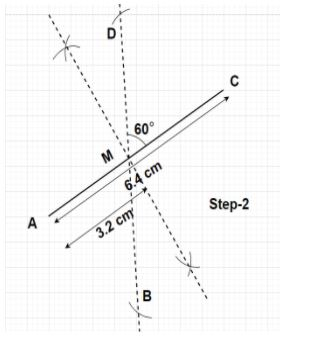
Step3- Now, join points A and B together, B and C together, C and D together, D and A together through a straight line using a scale. This ABCD is the required parallelogram with AC of length 6.4 cm and BD of length 8.2 cm as the diagonals. Here, the side AB is parallel to side CD and the side BC is parallel to the side AD.

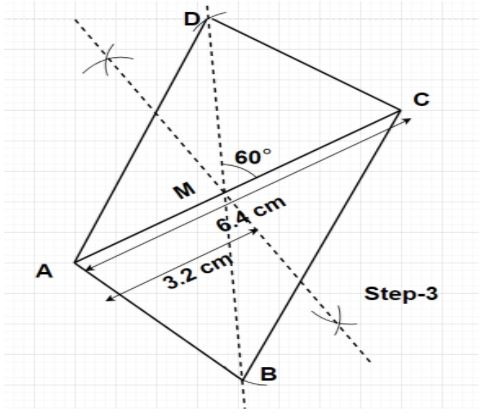
Now, if we will measure the length of the sides of this parallelogram ABCD using scale, we will find that AB=CD=3.7 cm and BC=AD=6.3 cm.
The perimeter of the constructed parallelogram is calculated by adding the length of all the sides i.e., Perimeter of parallelogram ABCD = AB+BC+CD+AD = 3.7+6.3+3.7+6.3 = 20 cm.
Therefore, the perimeter of the parallelogram ABCD is equal to 20 cm.

Note: In this particular problem, we have obtained the midpoint M of the diagonal AC by opening the ends of the compass more than half of the length of diagonal AC (i.e., the distance between the ends of the compass is more than 3.2 cm) and then by placing the fixed end at point A and then at point B respectively, these arcs will intersect at two distinct points. Join these points by a dotted line and this dotted line intersects the diagonal AC at the midpoint of AC i.e., point M.