Question

Construct a direct common tangent to two circles of radii 4cm and 2cm whose centers are 8cm apart. Measure and verify the length of the tangent.

Answer 1

Hint: In this particular type of question use the concept that if the center of the circle are apart by a distance and the radius of the circles are given than the length of the common tangent is given as the square root of the difference of the square of the distance between the centers and the square of the difference of the radii of the circles so use this concept to reach the solution of the question.

Complete step-by-step answer:
The radii of given circles is 4 cm and 2 cm respectively.
Now first draw the circle with radii 4 and O is the center.

Now make a horizontal straight line of 8cm from the center of the circle, mark the other end point of this line as O’ as shown in the figure.

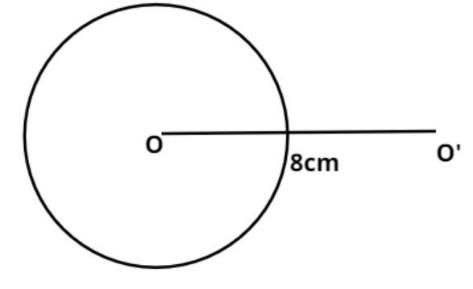
Now draw the circle of radii 2 cm with center O’.

Now draw the perpendicular bisector of line OO’ which cut the line at point A, as shown in the figure.

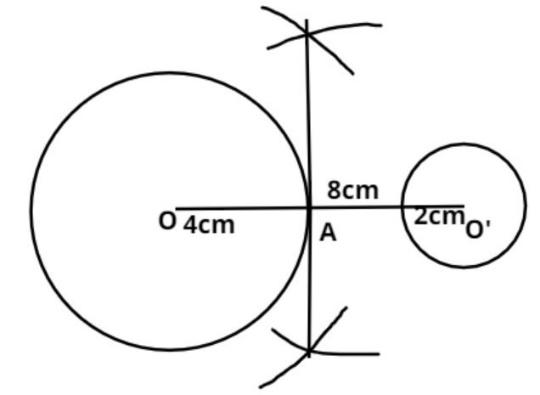
Now draw the circle with point A as center and AO is the radius as shown in the figure.

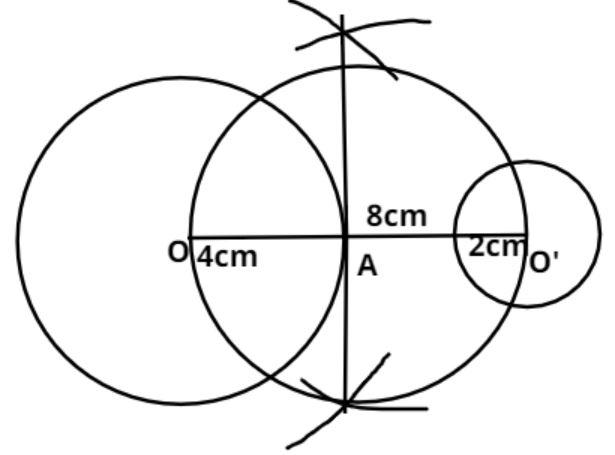
Now draw another circle with point O as center and radius is the difference of given circle radius = (4 – 2) = 2cm, as shown in the figure.

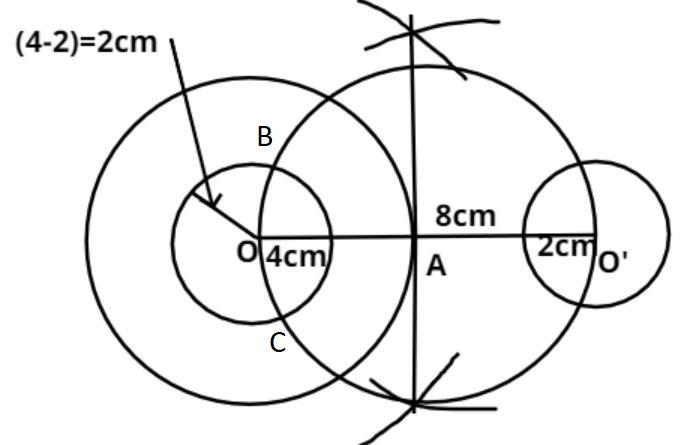
Now this circle cuts the circle which has radius AO at point B and C respectively as shown in the figure.
Now join point OB and OC and extend then such that it cuts the bigger circle at point D and E.

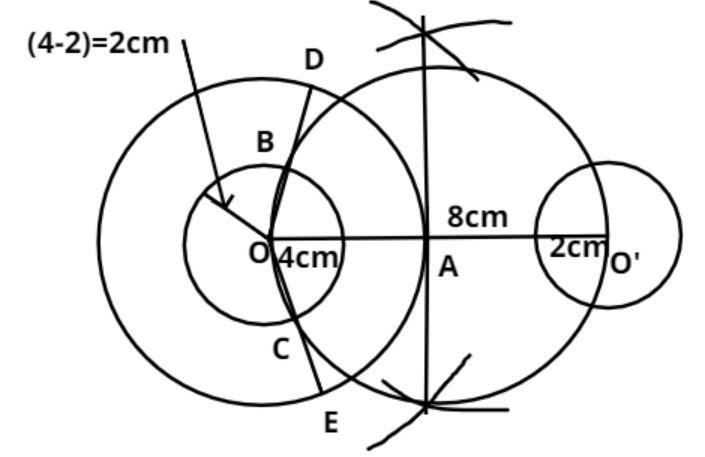
Now draw O’F and O’G parallel to OD and OE as shown in the figure.

Now join D and F and join E and G.

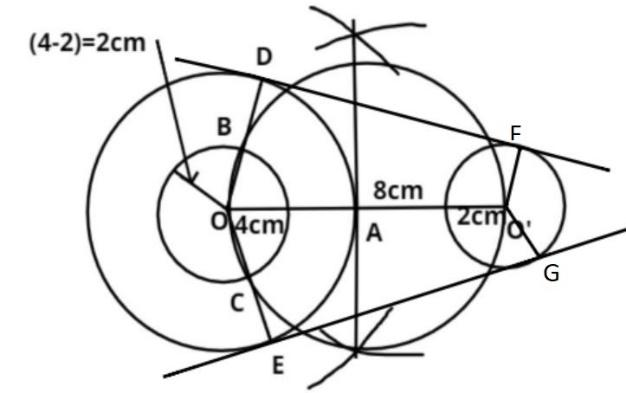
So DF and EG are the required direct common tangent to two given circles.
Now if we measure the length of this tangent by a scale it comes out 7.75cm.
Now we have to verify this.
Now as we know that the length of the common tangent DF is given as,
$ \Rightarrow {\left( {DF} \right)^2} = {\left( {OO'} \right)^2} - {\left( {OD - O'F} \right)^2}$
Where DF = length of tangent, OO’ = 8 cm (distance between the centers of the circle), OD = 4cm radius of the bigger circle and O’F = 2cm radius of the smaller circle.
$ \Rightarrow {\left( {DF} \right)^2} = {\left( 8 \right)^2} - {\left( {4 - 2} \right)^2}$
$ \Rightarrow {\left( {DF} \right)^2} = 64 - 4 = 60$
$ \Rightarrow DF = \sqrt {60} = 7.75$Cm.
So this is the required answer.
Hence verified.

Note – Whenever we face such types of questions the key concept we have to remember is that always recall the steps of the construction which is stated above these steps are the basis of the construction without these steps we cannot construct the common tangent to two circles of radii 4cm and 2cm.