Question

Construct a $\Delta ABC$ with $AB=3cm,BC=4cm$ and $AC=5cm$ and find a measure of $m\angle ABC$.
(A)$30{}^\circ $
(B)$53{}^\circ $
(C)$43{}^\circ $
(D)$90{}^\circ $

Answer 1

Hint: Observe the relation among the sides of the given triangle. Pythagoras theorem is for a right angled triangle and expressed as
${{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$
Use the above mentioned property of a right angle triangle and relate it with the given triangle with the help of sides.

Complete step-by-step answer:
We have a $\Delta ABC$ with sides AB of 3cm, BC of 4cm and AC of 5cm and we need to determine the measure of angle $\angle ABC$.

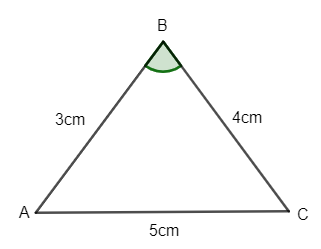
Here, let us try to observe the relation among the lengths of sides of $\Delta ABC$. We have
$AB=3cm,BC=4cm,AC=5cm$

Let us calculate the value of $A{{B}^{2}}+B{{C}^{2}}$ from the given triangle. Hence, we get

$A{{B}^{2}}+B{{C}^{2}}={{\left( 3 \right)}^{2}}+{{\left( 4 \right)}^{2}}$

$=9+14$

$A{{B}^{2}}+B{{C}^{2}}=25$ ……………………………………….(i)

And hence, we can observe that the value of ${{\left( AC \right)}^{2}}$ can be given 25 as length AC is of 5 cm. So, we get

${{\left( AC \right)}^{2}}=25$ …………………………………………(ii)

Now, we can equate the left hand sides of the equation (i) and (ii) as the right hand sides of them are equal. So, we get

${{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}}$ ……………………………………(iii)

Now, we know the Pythagoras theorem for a right angle triangle is defined by the relation

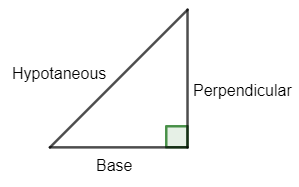
${{\left( hypotenuse \right)}^{2}}={{\left( perpendicular \right)}^{2}}+{{\left( base
\right)}^{2}}$ ……………………………….(iv)
Where the opposite angle of hypotenuse is $90{}^\circ $.
Hence, on comparing the relations (iii) and (iv), we get that (AC) is acting as a hypotenuse for the $\Delta ABC$. Hence the measure of the angle B should be $90{}^\circ $ to follow the Pythagoras rule.
Hence, we get $m\angle ABC=90{}^\circ $
So, option (D) is the correct answer.

Note: Another approach for calculating the angle A in $\Delta ABC$ would be applying the cosine identity in terms of length. It is given as
$\cos \theta =\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
Where a, b, c are sides and $\theta $ is the angle between ‘b’ and ‘c’. So, we get
$\cos A=\dfrac{{{3}^{2}}+{{4}^{2}}-{{5}^{2}}}{2\times 3\times 4}=0$
Hence, $A=\dfrac{\pi }{2}\Rightarrow 90{}^\circ $
Observing the Pythagoras pattern with the given triangle is the key point of the question and solution as well.
One needs to be clear with the Pythagoras theorem. Place of the terms hypotenuse, base and perpendicular are fixed, it will not change. So, be careful with the identity of it as well.