Question

Consider two different cloth – cutting processes. In the first one, n circular cloth pieces are cut from a square cloth piece of side ‘a’ in the following steps: the original square of side ‘a’ is divided into n smaller squares, not necessarily of the same size; then a circle of the maximum possible area is cut from each of the smaller squares. In the second process, only one circle of the maximum possible area is cut from the square of side ‘a’ and the process ends there. The cloth pieces remaining after cutting the circles are scrapped in both the processes. The ratio of the total area of the scrap cloth generated in the former to that in the later is:
(a) 1:1
(b) \[\sqrt{2}:1\]
(c) \[\dfrac{n\left( 4-\pi \right)}{4n-\pi }\]
(d) \[\dfrac{4n-\pi }{n\left( 4-\pi \right)}\]

Answer 1

Hint: To solve this question, we should know few formulas of mensuration like the area of the square is calculated by squaring the sides of the square, that is \[{{\left( s \right)}^{2}}\] and the area of the circle is calculated by multiplying the square of the radius with the pi, that is \[\pi {{r}^{2}}\]. By these formulas and the basic knowledge of ratio, we will be able to find the ratio.

Complete step-by-step answer:
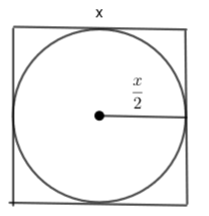
In this question, we have to find the ratio of the total scrap generated by both the processes. We will consider a square of side x and then we will find the area of that square, that is,
Area of square = side \[\times \] side
Area of square \[={{\left( x \right)}^{2}}\]
Now, we will cut the largest circle possible from the square of side x. So, the radius of the circle will be \[\left( \dfrac{x}{2} \right)\]. Therefore, the area of the circle will be
Area of the circle = \[\pi {{r}^{2}}\]
Area of the circle = \[\pi {{\left( \dfrac{x}{2} \right)}^{2}}\]
Area of the circle \[=\dfrac{\pi {{x}^{2}}}{4}\]

Now we will calculate the area of the scrap generated by cutting the piece of the circle from the square by using the formula.
Area of scrap = Area of the square – Area of the circle
Area of scrap \[={{x}^{2}}-\dfrac{\pi {{x}^{2}}}{4}\]
Area of scrap \[={{x}^{2}}\left( 1-\dfrac{\pi }{4} \right)\]
Now, we will divide the whole equation by \[{{x}^{2}}\]. So, we get,
\[\dfrac{\text{Area of scrap}}{{{x}^{2}}}=\dfrac{{{x}^{2}}}{{{x}^{2}}}\left( 1-\dfrac{\pi }{4} \right)\]
\[\dfrac{\text{Area of scrap}}{{{x}^{2}}}=\left( 1-\dfrac{\pi }{4} \right)\]
where \[{{x}^{2}}\] is the area of the square. So, we can write it as,
\[\dfrac{\text{Area of scrap}}{\text{Area of the square}}=1-\dfrac{\pi }{4}\]
From this, we can see that the ratio of the area of scrap to the ratio of the area of the square is always constant whether we cut the circle from a smaller square or larger square that means the scrapped area is always a fixed percentage of the square.
In this question, we have taken both squares of equal size. So, the ratio of the scrapped area will also be equal. Therefore we can say that the ratio of the scrap area in both the processes is equal, that means, in the ratio of 1:1.
Hence, option (a) is the right answer.

Note: The possible mistake one can make is assuming different cases for process 1 and then finding the ratio of the scrapped area generated in the former to that in the latter. It is not wrong, but this will make the solution more lengthy and complicated.