Question

Consider the shown mechanism ABC. At a certain instant shown in diagram block C was found to be moving with speed of \[1m/s\]to the right. At this instant what is the magnitude of the vertical component of velocity B.

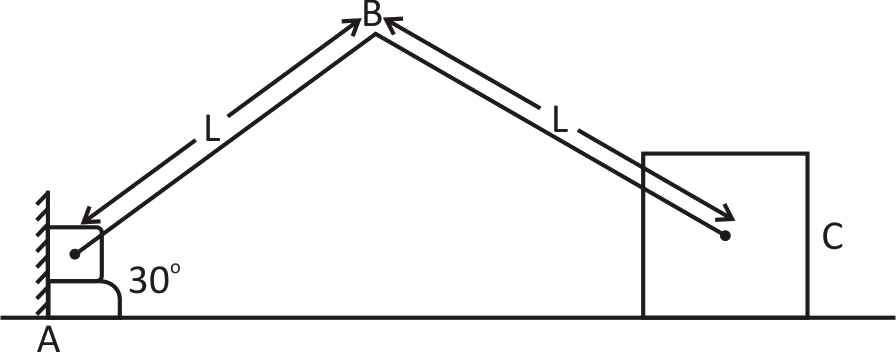
(A)\[\dfrac{1}{2}m/s\]
(B) \[\dfrac{{\sqrt 3 }}{2}m/s\]
(C) \[\dfrac{{\sqrt 3 }}{4}m/s\]
(D) \[2\sqrt 3 m/s\]

Answer 1

Hint: In this question, block C is moving with a speed of \[1m/s\] to the right direction. By taking the angles into consideration we can find the velocity along BC we can take the vertical component of Velocity. By substituting the value of angle and velocity, we can easily determine the value of the vertical component of velocity B.

Complete step by step solution:
For finding the vertical component of velocity B, Firstly we need to find by which velocity BC is moving.

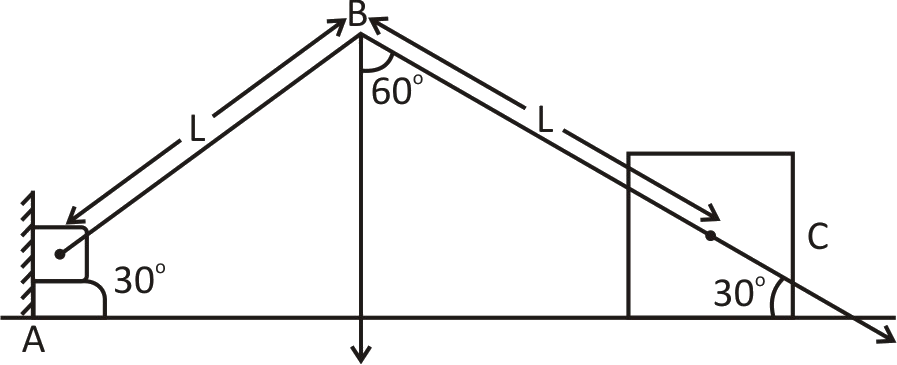
As already given in the question, that block is moving with speed of \[1m/s\] to the right.
So, velocity along BC will be-
\[{V_X}\operatorname{Cos} {30^ \circ } = 1 \times \dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{2}m/\sec \]
Now, for calculating the vertical component of velocity at B. We know that vertical component will be-\[{V_y}\operatorname{Cos} \theta \]
Here θ is 60° along the vertical component of Velocity, so-
\[V\operatorname{Cos} {60^ \circ } = \dfrac{{\sqrt 3 }}{2} \times \dfrac{1}{2} = \dfrac{{\sqrt 3 }}{4}m/\sec \]
So, magnitude of vertical component of velocity B is- \[\dfrac{{\sqrt 3 }}{4}m/\sec \]

So, the correct answer is “Option C”.

Note:
By breaking the diagonal velocity into horizontal and vertical components makes it easy for us to deal with each direction separately. This method of breaking up the vectors into its horizontal and vertical components works even when the vector is other than velocity such as force and momentum.