Question

Consider the motion of a positive point charge in a region where there are simultaneous uniform electric and magnetic fields \[\overrightarrow{E}={{E}_{0}}\widehat{j}\text{ }and\text{ }\overrightarrow{B}={{B}_{0}}\widehat{j}.\] At time \[t=0\], this charge has velocity \[\overrightarrow{v}\] in the x-y plane, making an angle \[\theta \] with the x-axis. Which of the following is /(are) correct for time \[t>0\]?
A.If \[\theta ={{0}^{0}}\], the charge moves in a circular path in the x-z plane.
B.If \[\theta ={{0}^{0}}\], the charge undergoes helical motion with constant pitch along the y-axis.
C.If \[\theta ={{10}^{0}}\], the charge undergoes helical motion with its pitch increasing with time, along the z-axis.
D.If \[\theta ={{90}^{0}}\], the charge undergoes linear but accelerated motion along the y-axis.

Answer 1

Hint: The electric field and magnetic field together contributes to the state of motion of the point charge. The direction of motion is determined by the charge of the particle, which is positive here. The EF and MF determines the type of motion in the plane.

Complete answer:
Let us consider the forces acting on a charged particle due to the Electric and magnetic fields.
Due to electric field a charged particle experience, \[F=q\overrightarrow{E}\]
Due to magnetic field a charged particle experience, \[F=q(\overrightarrow{v}\times \overrightarrow{B})\]
From the above expressions we can understand that for charged particles experiencing both the fields along the same direction, as given here, the particle experiences force in two directions which are perpendicular. Let us illustrate this condition in a figure
  

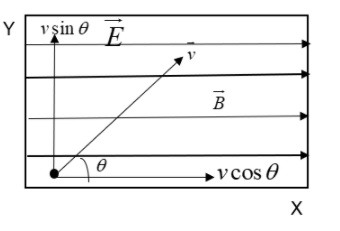
The force due to the electric field is along the x-axis and the force due to the magnetic field is along the z-axis.
Let us consider different values of angle,
At \[\theta ={{0}^{0}}\], The force due to the magnetic field will result in a circular motion, but the electric field forces it along the x-axis. This means that the particle undergoes a helical path. The pitch (the horizontal component of the velocity) varies with time
At \[\theta ={{10}^{0}}\], due to the magnetic field cosine component of the velocity, there exists a pitch. But also due to the sine component of velocity and electric field the pitch is interrupted periodically. i.e., the particle has a variable pitch and has an accelerated motion.
At \[\theta ={{90}^{0}}\], the force due to the magnetic field is zero. As a result the particle undergoes accelerated motion along the y-axis.

From the above observations, we can conclude that the correct answers are given by options C and D.

Additional Information:
The pitch of a charged particle is given by -
\[Pitch=v\cos \theta \times Time\text{ period}\]

Note:
It is often confusing when non-charged particles are kept in electric and magnetic fields. Only charged particles can experience a force in any of these fields, given that they are not changing with time. A changing field can induce another field and thereby a force.